《2025年课堂点睛九年级数学上册人教版宁夏专版》

8.如图是一张长12cm,宽10cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积是$24cm^{2}$的有盖的长方体铁盒,则剪去的正方形的边长为2cm.

答案： 2

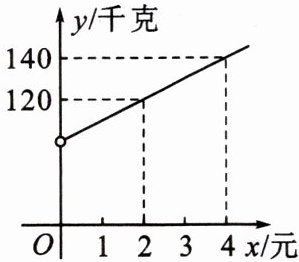
9.(银川市英才学校期中)某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售.为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)$(0＜x＜20)$之间满足一次函数关系,其图象如图所示:
(1)求y与x之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?

答案：
(1)设一次函数解析式为y=kx+b.
∵当x=2时,y=120;当x=4时,y=140;
∴{2k+b=120,4k+b=140.解得{k=10,b=100.
∴y与x之间的函数关系式为y=10x+100.
(2)由题意,得(60-40-x)(10x+100)=2090.整理,得x²-10x+9=0,解得x₁=1,x₂=9.
∵让顾客得到更大的实惠,
∴x=9.答:商贸公司要想获利2090元,则这种干果每千克应降价9元.

10.若方程$(a-1)x^{a^{2}+1}+3x= 1$是关于x的一元二次方程,则a的值是-1.

答案： -1

11.α、β是关于x的方程$x^{2}-x+k-1= 0$的两个实数根,且$α^{2}-2α-β= 4$,则k的值为-4.

答案： -4

12.(宁夏自治区中考)关于x的一元二次方程$(a-1)x^{2}+3x-2= 0$有实数根,则a的取值范围是(D)
A.$a＞-\frac {1}{8}$
B.$a≥-\frac {1}{8}$
C.$a＞-\frac {1}{8}且a≠1$
D.$a≥-\frac {1}{8}且a≠1$

答案： D

13.(固原弘文中学期中)阅读材料:
材料1:若关于x的一元二次方程$ax^{2}+bx+c= 0(a≠0)的两个根为x_{1},x_{2}$,则$x_{1}+x_{2}= -\frac {b}{a},$$x_{1}x_{2}= \frac {c}{a}.$
材料2:已知一元二次方程$x^{2}-x-1= 0$的两个实数根分别为m,n,求$m^{2}n+mn^{2}$的值.
解:∵一元二次方程$x^{2}-x-1= 0$的两个实数根分别为m,n,$\therefore m+n= 1,mn= -1,则m^{2}n+mn^{2}= mn(m+n)= -1×1= -1.$
根据上述材料,结合你所学的知识,完成下列问题:
(1)材料理解:一元二次方程$2x^{2}-3x-1= 0的两个根为x_{1},x_{2}$,则$x_{1}+x_{2}= $3/2,$x_{1}x_{2}= $-1/2.
(2)类比应用:已知一元二次方程$2x^{2}-3x-1= 0$的两根分别为m、n,求$\frac {n}{m}+\frac {m}{n}$的值.
∵一元二次方程2x²-3x-1=0的两根分别为m、n,
∴m+n=3/2,mn=-1/2,
∴n/m + m/n=(n²+m²)/mn=((m+n)²-2mn)/mn=((3/2)²-2×(-1/2))/(-1/2)=-13/2.
(3)思维拓展:已知实数s、t满足$2s^{2}-3s-1= 0,2t^{2}-3t-1= 0$,且$s≠t$,则$\frac {1}{s}-\frac {1}{t}= $±√17.

答案：
(1)3/2 -1/2
(2)
∵一元二次方程2x²-3x-1=0的两根分别为m、n,
∴m+n=3/2,mn=-1/2,
∴n/m + m/n=(n²+m²)/mn=((m+n)²-2mn)/mn=((3/2)²-2×(-1/2))/(-1/2)=-13/2.
(3)±√17