《2025年课堂点睛九年级数学上册人教版宁夏专版》

8. (宁夏自治区中考)已知正三角形ABC的边长为6,那么能够完全覆盖这个正三角形ABC的最小圆面的半径是$2\sqrt{3}$.

答案： $2\sqrt{3}$

9. (玉林市中考)如图,在$5×7$网格中,各小正方形边长均为1,点O,A,B,C,D,E均在格点上,点O是$\triangle ABC$的外心,在不添加其他字母的情况下,则除$\triangle ABC$外把你认为外心也是O的三角形都写出来______.

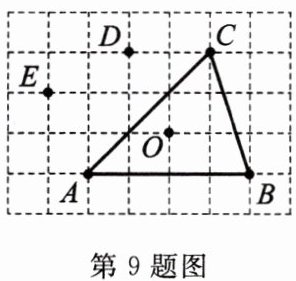
答案： △ABD,△ACD,△BCD

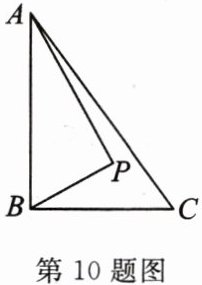
10. 如图,在$Rt\triangle ABC$中,$AB\perp BC,AB= 6,BC= 4$,P是$\triangle ABC$内部的一个动点,且满足$\angle PAB+\angle PBA= 90^{\circ}$,则线段CP长的最小值为______2.

答案： 2

11. 已知$\odot O_{1}$过坐标原点O,点$O_{1}的坐标为(1,1)$,试判断点$P(-1,1),Q(1,0),R(2,2)与\odot O_{1}$的位置关系,并说明理由.

答案： 解:⊙O₁的半径r=√2,PO₁=2＞√2,QO₁=1＜√2,RO₁=√2,故点P在⊙O₁外,点Q在⊙O₁内,点R在⊙O₁上.

12. 如图,在$\triangle ABC$中,$\angle ACB= 90^{\circ},AB= 10,BC= 8,CD\perp AB$于点D,O为AB的中点.
(1)以C为圆心,6为半径作$\odot C$,试判断点A,D,B与$\odot C$的位置关系;
(2)$\odot C$的半径为多少时,点O在$\odot C$上?

答案： 解:在△ABC中,∠ACB=90°,AB=10,BC=8,CD⊥AB,由勾股定理得AC=6.由三角形面积公式得S_{△ABC}=1/2AC·BC=1/2AB·CD,
∴CD=4.8.
(1)
∵AC=6,
∴点A在⊙C上.
∵BC=8＞6,
∴点B在⊙C外.
∵CD=4.8＜6,
∴点D在⊙C内.
(2)
∵点O为AB的中点,∠ACB=90°,
∴OC=1/2AB=5.
∴⊙C的半径为5时,点O在⊙C上.

13. (核心素养·推理能力)(石嘴山二中月考)如图,AD为$\triangle ABC$外接圆的直径,$AD\perp BC$,垂足为F,$\angle ABC$的平分线交AD于点E,连接BD,CD.
(1)求证:$BD= CD$.
(2)请判断B,E,C三点是否在以点D为圆心、DB长为半径的圆上,并说明理由.

答案：
(1)证明:
∵AD为△ABC外接圆的直径,AD⊥BC,
∴弧BD=弧CD.
∴BD=CD.
(2)解:B,E,C三点在以点D为圆心、DB长为半径的圆上.理由如下:由
(1)知,弧BD=弧CD.
∴∠BAD=∠CBD.
∵BE平分∠ABC,
∴∠CBE=∠ABE.又
∵∠DBE=∠CBD+∠CBE,∠DEB=∠BAD+∠ABE,
∴∠DBE=∠DEB.
∴DB=DE.由
(1)知,BD=CD.
∴DB=DE=DC.
∴B,E,C三点在以点D为圆心、DB长为半径的圆上.