第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
【例】(宁夏自治区中考改编)2022 北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度 OA 为4米,以起跳点正下方跳台底端 O 为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点 B 的坐标为(4,12),着陆坡顶端 C 与落地点 D 的距离为 2.5米,若$\frac {CE}{DE}= \frac {3}{4}.$
(1)求点 A 的坐标;
(2)求该抛物线的函数解析式;
(3)起跳点 A 与着陆坡顶端 C 之间的水平距离 OC 的长.(精确到0.1米,参考数据:$\sqrt {3}\approx 1.73$)
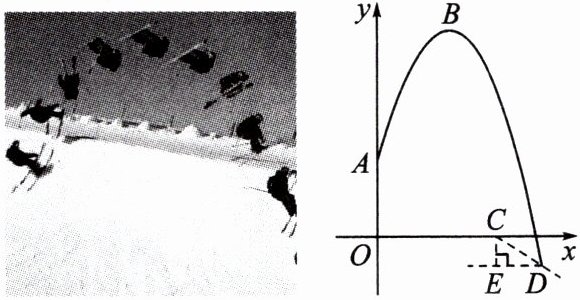
(1)求点 A 的坐标;
(2)求该抛物线的函数解析式;
(3)起跳点 A 与着陆坡顶端 C 之间的水平距离 OC 的长.(精确到0.1米,参考数据:$\sqrt {3}\approx 1.73$)

答案:
(1)
∵OA=4,且点A在y轴正半轴,
∴A(0,4).
(2)
∵抛物线最高点B的坐标为(4,12),
∴设抛物线的解析式为y=a(x-4)²+12,
∵A(0,4),
∴a(0-4)²+12=4,解得$a=-\dfrac{1}{2}.$
∴抛物线的解析式为$y=-\dfrac{1}{2}(x-4)²+12. (3)$在Rt△CDE中$,\dfrac{CE}{DE}=\dfrac{3}{4},CD=2.5,$
∴CE=1.5,DE=2,
∴点D的纵坐标为-1.5,令$-\dfrac{1}{2}(x-4)²+12=-1.5,$解得x₁=4+3√3≈9.19,x₂=4-3√3≈-1.19(不合题意,舍去),
∴D(9.19,-1.5).
∴OC=9.19-2=7.19≈7.2(m).
∴OC的长约为7.2米.
(1)
∵OA=4,且点A在y轴正半轴,
∴A(0,4).
(2)
∵抛物线最高点B的坐标为(4,12),
∴设抛物线的解析式为y=a(x-4)²+12,
∵A(0,4),
∴a(0-4)²+12=4,解得$a=-\dfrac{1}{2}.$
∴抛物线的解析式为$y=-\dfrac{1}{2}(x-4)²+12. (3)$在Rt△CDE中$,\dfrac{CE}{DE}=\dfrac{3}{4},CD=2.5,$
∴CE=1.5,DE=2,
∴点D的纵坐标为-1.5,令$-\dfrac{1}{2}(x-4)²+12=-1.5,$解得x₁=4+3√3≈9.19,x₂=4-3√3≈-1.19(不合题意,舍去),
∴D(9.19,-1.5).
∴OC=9.19-2=7.19≈7.2(m).
∴OC的长约为7.2米.
1.(兰州市中考)掷实心球是兰州市高中阶段学校招生体育考试的选考项目.如图1是一名女生投掷实心球,实心球行进路线是一条抛物线,行进高度 y(m)与水平距离 x(m)之间的函数关系如图2所示,抛出时起点处高度为$\frac {5}{3}m$,当水平距离为3m时,实心球行进至最高点3m处.
(1)求 y 关于 x 的函数解析式;
(2)根据兰州市高中阶段学校招生体育考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.70m,此项考试得分为满分10分.该女生在此项考试中是否得满分,请说明理由.
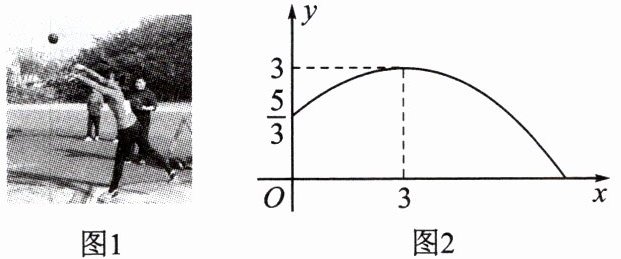
(1)求 y 关于 x 的函数解析式;
(2)根据兰州市高中阶段学校招生体育考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.70m,此项考试得分为满分10分.该女生在此项考试中是否得满分,请说明理由.

答案:
(1)当水平距离为3m时,实心球行进至最高点3m处,
∴设y=a(x-3)²+3,
∵y=a(x-3)²+3经过点$(0,\dfrac{5}{3}),$
∴$\dfrac{5}{3}=a(0-3)²+3,$
∴$a=-\dfrac{4}{27},$
∴$y=-\dfrac{4}{27}(x-3)²+3=-\dfrac{4}{27}x²+\dfrac{8}{9}x+\dfrac{5}{3},$
∴y关于x的函数解析式为$y=-\dfrac{4}{27}x²+\dfrac{8}{9}x+\dfrac{5}{3}. (2)$该女生在此项考试中是得满分,理由如下:
∵对于二次函数$y=-\dfrac{4}{27}x²+\dfrac{8}{9}x+\dfrac{5}{3},$当y=0时,有$-\dfrac{4}{27}x²+\dfrac{8}{9}x+\dfrac{5}{3}=0,$
∴4x²-24x-45=0,解得$x₁=\dfrac{15}{2},x₂=-\dfrac{3}{2}($舍去).
∵$\dfrac{15}{2}>6.70,$
∴该女生在此项考试中时得满分.)
(1)当水平距离为3m时,实心球行进至最高点3m处,
∴设y=a(x-3)²+3,
∵y=a(x-3)²+3经过点$(0,\dfrac{5}{3}),$
∴$\dfrac{5}{3}=a(0-3)²+3,$
∴$a=-\dfrac{4}{27},$
∴$y=-\dfrac{4}{27}(x-3)²+3=-\dfrac{4}{27}x²+\dfrac{8}{9}x+\dfrac{5}{3},$
∴y关于x的函数解析式为$y=-\dfrac{4}{27}x²+\dfrac{8}{9}x+\dfrac{5}{3}. (2)$该女生在此项考试中是得满分,理由如下:
∵对于二次函数$y=-\dfrac{4}{27}x²+\dfrac{8}{9}x+\dfrac{5}{3},$当y=0时,有$-\dfrac{4}{27}x²+\dfrac{8}{9}x+\dfrac{5}{3}=0,$
∴4x²-24x-45=0,解得$x₁=\dfrac{15}{2},x₂=-\dfrac{3}{2}($舍去).
∵$\dfrac{15}{2}>6.70,$
∴该女生在此项考试中时得满分.)
查看更多完整答案,请扫码查看


