《2025年课堂点睛九年级数学上册人教版宁夏专版》

1. 如图,A是$\odot O$上一点,且$PA= 12$,$PB= 8$,$OB= 5$,则PA与$\odot O$的位置关系是相切.

答案： 相切

2. 如图,AB是$\odot O$的直径,BC是$\odot O$的弦,D为BA延长线上一点,$\angle B= 25^\circ$,当$\angle D$等于40°时,CD与$\odot O$相切.

答案： 40°

3. 如图,AB是$\odot O$的直径,点C为$\odot O$上一点,过点B作$BD\perp CD$,垂足为点D,连接BC,BC平分$\angle ABD$.求证:CD为$\odot O$的切线.

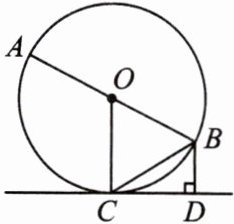
答案： 证明:
∵BC平分∠ABD,
∴∠OBC = ∠DBC,
∵OB = OC,
∴∠OBC=∠OCB,
∴∠OCB = ∠DBC,
∴OC//BD
∵BD⊥CD,
∴OC⊥CD
∵OC是⊙O 的半径,
∴CD为⊙O的切线

4. (河池市中考)如图,AB是$\odot O$的直径,PA与$\odot O$相切于点A,$\angle ABC= 25^\circ$,OC的延长线交PA于点P,则$\angle P$的度数是(C)
A.$25^\circ$
B.$35^\circ$
C.$40^\circ$
D.$50^\circ$

答案： C

5. (无锡市中考)如图,AB是$\odot O$的直径,$AB= 6$,BC是$\odot O$的切线,D是AC的中点,$OD= 2$,则AC的值为(D)
A.10
B.8
C.$2\sqrt{15}$
D.$2\sqrt{13}$

答案： D

6. (金华市中考)如图,木工用角尺的短边紧靠$\odot O$于点A,长边与$\odot O$相切于点B,角尺的直角顶点为C.已知$AC= 6\mathrm{cm}$,$CB= 8\mathrm{cm}$,则$\odot O$的半径为$\frac{25}{3}$cm.

答案： $\frac{25}{3}$

7. 如图,PO平分$\angle MPN$,$\odot O$与PM相切于点A.求证:PN是$\odot O$的切线.

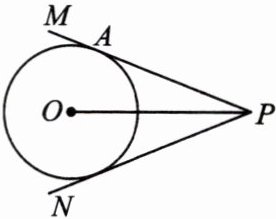
答案：
解:连接OA,作OB⊥PN于点B, 则∠OBP = 90°.
∵⊙O与PM相切于点A,
∴∠OAP = 90°.
∴∠OAP=∠OBP.又
∵∠OPA=∠OPB,OP = OP,
∴△AOP≌△BOP(AAS).
∴OB = OA,即OB是⊙O的半径,
∴PN是⊙O的切线.

8. 如图,$\odot O与\triangle OAB$的边AB相切,切点为B,将$\triangle OAB$绕点B按顺时针方向旋转得到$\triangle O'A'B$,使点$O'落在\odot O$上,边$A'B$交线段AO于点C,若$\angle A'= 25^\circ$,则$\angle OCB= $85度.

答案： 85