第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.(甘肃省中考)如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧($\overset{\frown}{AB}$),点O是这段弧所在圆的圆心,半径OA= 90m,圆心角∠AOB= 80°,则这段弯路($\overset{\frown}{AB}$)的长度为(

A.20πm
B.30πm
C.40πm
D.50πm
C
)
A.20πm
B.30πm
C.40πm
D.50πm
答案:
C
2.在活动课上,“雄鹰组”用含30°角的直角三角尺设计风车,如图,∠C= 90°,∠ABC= 30°,AC= 2,将直角三角尺绕点A逆时针旋转得到△AB'C',使点C'落在AB边上,以此方法做下去……则B点通过一次旋转至B'所经过的路径长为
$\frac{4\pi}{3}$
.(结果保留π)
答案:
$\frac{4\pi}{3}$
3.(兰州市中考)如图,传送带的一个转动轮的半径为18cm,转动轮转n°,传送带上的物品A被传送12πcm,则n=
120
.
答案:
120
4.一个扇形的半径为6,圆心角为120°,则这个扇形的面积是(
A.2π
B.4π
C.12π
D.24π
C
)A.2π
B.4π
C.12π
D.24π
答案:
C
5.如图,△ABC是⊙O的内接正三角形,⊙O的半径为3,则图中阴影部分的面积是(
A.π
B.2π
C.3π
D.4π
C
)A.π
B.2π
C.3π
D.4π
答案:
C
6.(宁夏自治区中考)已知扇形的圆心角为100°,所对的弧长为$\frac{5\pi}{3}$,则此扇形的面积是
$\frac{5}{2}\pi$
.
答案:
$\frac{5}{2}\pi$
7.(教材第112页例2变式)如图,已知⊙O的周长为4π,$\overset{\frown}{AB}$的长为π,求图中阴影部分的面积.
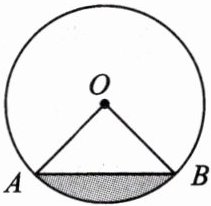

答案:
解:
∵$\odot O$的周长为$4\pi$,
∴$\odot O$的半径$r = 4\pi÷2\pi = 2$。
∵$\overset{\frown}{AB}$的长为$\pi$,
∴$\overset{\frown}{AB}$的长等于$\odot O$的周长的$\frac{1}{4}$。
∴$\angle AOB = 90^{\circ}$。
∴$S_{阴影}=\frac{1}{4}\pi×2^{2}-2×2×\frac{1}{2}=\pi - 2$。
∵$\odot O$的周长为$4\pi$,
∴$\odot O$的半径$r = 4\pi÷2\pi = 2$。
∵$\overset{\frown}{AB}$的长为$\pi$,
∴$\overset{\frown}{AB}$的长等于$\odot O$的周长的$\frac{1}{4}$。
∴$\angle AOB = 90^{\circ}$。
∴$S_{阴影}=\frac{1}{4}\pi×2^{2}-2×2×\frac{1}{2}=\pi - 2$。
8.如图,将⊙O沿弦AB折叠,$\overset{\frown}{AB}$恰好经过圆心O,若⊙O的半径为3,则$\overset{\frown}{AB}$的长为(
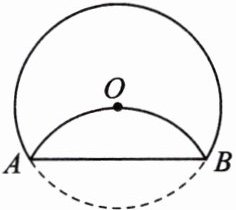
A.$\frac{1}{2}\pi$
B.π
C.2π
D.3π
C
)
A.$\frac{1}{2}\pi$
B.π
C.2π
D.3π
答案:
C
9.(河北省中考)某款“不倒翁”(图1)的主视图是图2,PA,PB分别与$\overset{\frown}{AMB}$所在圆相切于点A,B,若该圆半径是9cm,∠P= 40°,则$\overset{\frown}{AMB}$的长是(
A.11πcm
B.$\frac{11}{2}\pi$cm
C.7πcm
D.$\frac{7}{2}\pi$cm
A
)A.11πcm
B.$\frac{11}{2}\pi$cm
C.7πcm
D.$\frac{7}{2}\pi$cm
答案:
A
查看更多完整答案,请扫码查看


