《2025年课堂点睛九年级数学上册人教版宁夏专版》

1.用长8m的铝合金条制成使窗户的透光面积最大的矩形窗框(如图),那么这个窗户的最大透光面积是(C)
A.$\frac{64}{25}\text{m}^2$
B.$\frac{4}{3}\text{m}^2$
C.$\frac{8}{3}\text{m}^2$
D.$4\text{m}^2$

答案： C

2.如图,利用一个直角墙角修建一个梯形储料场ABCD,其中$\angle C= 120^\circ$.若新建墙BC与CD总长为12m,则该梯形储料场ABCD的最大面积是$\underline{\quad\quad}m^2$.
24√3

答案： 解：设CD的长为$x$m，则BC的长为$(12 - x)$m。
过点C作CE⊥AB于点E，过点C作CF⊥AD于点F。
因为∠D=∠A=90°，所以四边形AFCD为矩形，故CF=AD，AF=CD=x m。
在Rt△CFD中，∠DCF=90°，∠BCD=120°，所以∠BCE=∠BCD - ∠DCF=120° - 90°=30°。
在Rt△BCE中，BC=(12 - x)m，∠BCE=30°，则BE=BC·sin30°=(12 - x)×$\frac{1}{2}$=$\frac{12 - x}{2}$m，CE=BC·cos30°=(12 - x)×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}(12 - x)}{2}$m。
所以AD=CF=CE=$\frac{\sqrt{3}(12 - x)}{2}$m，AB=AF + BE=x + $\frac{12 - x}{2}$=$\frac{x + 12}{2}$m。
梯形ABCD的面积$S=\frac{1}{2}(AB + CD)·AD$
=$\frac{1}{2}(\frac{x + 12}{2} + x)·\frac{\sqrt{3}(12 - x)}{2}$
=$\frac{1}{2}(\frac{3x + 12}{2})·\frac{\sqrt{3}(12 - x)}{2}$
=$\frac{\sqrt{3}(3x + 12)(12 - x)}{8}$
=$\frac{\sqrt{3}(-3x^{2} + 24x + 144)}{8}$
=-$\frac{3\sqrt{3}}{8}x^{2} + 3\sqrt{3}x + 18\sqrt{3}$
因为二次项系数-$\frac{3\sqrt{3}}{8}$＜0，所以当$x=-\frac{b}{2a}=-\frac{3\sqrt{3}}{2×(-\frac{3\sqrt{3}}{8})}$=4时，S有最大值。
将x=4代入S，得$S_{max}=-\frac{3\sqrt{3}}{8}×4^{2} + 3\sqrt{3}×4 + 18\sqrt{3}$=24$\sqrt{3}$
故该梯形储料场ABCD的最大面积是$24\sqrt{3}$m²。

3.(教材第52页第6题变式)如图,已知等腰直角$\triangle ABC$,$\angle C= 90^\circ$,$BC= 2cm$,在三角形内作矩形CDEF,使D在AC上,E在AB上,F在BC上,则矩形CDEF的最大面积为$\underline{\quad$1cm^2$\quad}$,此时矩形CDEF为$\underline{\quad正方形\quad}$.

答案： 【解析】：
本题考查了图形面积与二次函数的关系。通过设定矩形的一边长，利用相似三角形对应边成比例的关系，得出矩形另一边长的表达式，进而得出矩形面积的表达式，最后通过二次函数的性质求出矩形面积的最大值以及此时矩形的形状。
设$CF = x$厘米，
$\because\triangle ABC$是等腰直角三角形，$\angle C= 90^\circ$，$BC= 2\text{cm}$，
$\therefore AC = BC = 2$厘米，$\angle A = \angle B = 45^{\circ}$，
$\because$四边形$CDEF$是矩形，
$\therefore DE = CF = x$厘米，$EF = CD$，$DE// BC$，
$\therefore\angle ADE = \angle B = 45^{\circ}$，$\angle AED = \angle C = 90^{\circ}$，
$\therefore\triangle ADE$是等腰直角三角形，
$\therefore AD = DE = x$厘米，
$\therefore CD = EF = AC - AD = (2 - x)$厘米，
$\therefore$矩形$CDEF$的面积$S = CF× CD = x(2 - x)=-x^{2}+2x$，
$\because a = -1\lt 0$，
$\therefore$该函数图象开口向下，存在最大值，
根据二次函数性质，当$x = -\frac{b}{2a}=-\frac{2}{2×(-1)} = 1$时，$S$取得最大值，
$S_{最大值}=-\ 1^{2}+2× 1 = 1$（平方厘米），
此时$CF = EF = 1$厘米，
$\therefore$矩形$CDEF$是正方形。
【答案】：
$1\text{cm}^2$；正方形

4.如图,已知□ ABCD的周长为$8cm,\angle B= 30^\circ,$若边长AB= xcm.
(1)□ ABCD的面积$y(cm^2)$与x(cm)之间的函数解析式为$y=-\frac{1}{2} x^{2}+2x$,自变量x的取值范围为0＜x＜4;(2)当x取2时,y的值最大,最大值为2cm^{2}.

答案： 【解析】：
(1) 要求平行四边形ABCD的面积与$AB$边长$x$之间的函数关系。
已知平行四边形的一个角$\angle B=30^{\circ}$，周长为8cm，$AB=x$cm，
可以计算出$BC$的长度。
平行四边形的周长为$2(AB+BC)=8$，
所以$BC=\frac{8}{2}-x=4-x$，
过点A作$AE\perp BC$于E，
在$Rt \bigtriangleup ABE$中，
由于$\angle B=30^{\circ}$ ，
利用30度所对直角边等于斜边一半，
可得$AE=\frac{1}{2} AB=\frac{x}{2}$ ，
平行四边形的面积$y$可以表示为底乘以高，
即$y=BC× AE=(4-x) × \frac{x}{2}=-\frac{1}{2} x^{2}+2x$，
由于$AB$和$BC$都是边长，
所以它们必须大于0，
即$x＞0$且$4-x＞0$，
从而得出$x$的取值范围为$0＜x＜4$，
综上，函数解析式为：$y=-\frac{1}{2} x^{2}+2x$，自变量$x$的取值范围为$0＜x＜4$。
(2) 对于二次函数$y=ax^{2} +bx+c$，
当$a＜0$时，函数在$x=-\frac{b}{2a}$处取得最大值。
对于给定的函数$y=-\frac{1}{2} x^{2}+2x$，
有$a=-\frac{1}{2}$，$b=2$，
所以最大值出现在$x=-\frac{2}{2 × (-\frac{1}{2})}=2$处，
将$x=2$代入原函数，
得到最大值为$y=-\frac{1}{2} × 2^{2}+2 × 2=2$，
综上，当$x=2$时，$y$的值最大，最大值为$2cm^{2}$。
【答案】：
(1) $y=-\frac{1}{2} x^{2}+2x$；$0＜x＜4$；
(2) 2；$2cm^{2}$。

5.手工课上,小明准备做一个形状是菱形的风筝,这个菱形的两条对角线长度之和恰好为60cm,菱形的面积S(单位:$\text{cm}^2$)随其中一条对角线的长x(单位:cm)的变化而变化.
(1)请直接写出S与x之间的函数解析式(不要求写出自变量x的取值范围);
(2)当x是多少时,菱形风筝的面积S最大?最大面积是多少?

答案： 【解析】：
(1)设菱形的一条对角线长为$x$ cm，则另一条对角线的长为$(60 - x)$ cm。
菱形的面积公式为：$S = \frac{1}{2} × d_1 × d_2$，其中$d_1$和$d_2$是菱形的两条对角线长。
代入得：$S = \frac{1}{2} × x × (60 - x) = - \frac{1}{2}x^{2} + 30x$。
(2)为了求菱形面积的最大值，我们可以将上一步得到的函数解析式转化为顶点式。
$S = - \frac{1}{2}x^{2} + 30x = - \frac{1}{2}(x^{2} - 60x) = - \frac{1}{2}(x^{2} - 60x + 900) + 450 = - \frac{1}{2}(x - 30)^{2} + 450$。
由于二次项系数为负，所以这是一个开口向下的抛物线，其最大值出现在顶点处，即$x = 30$时，此时$S_{最大} = 450$ $\text{cm}^2$。
【答案】：
(1) $S = - \frac{1}{2}x^{2} + 30x$；
(2) 当$x$是$30$cm时，菱形风筝的面积$S$最大，最大面积是$450$ $\text{cm}^2$。

6.如图,用一段长为24m的篱笆围成一个一边靠墙的矩形养鸡场,若墙长8m,则这个养鸡场最大面积为$\underline{\quad64\quad}m^2$.

答案： 【解析】：本题考查图形面积与二次函数最值问题。
设养鸡场与墙垂直的一边长为$x$ m，由于篱笆总长为$24$m，且一边靠墙，所以与墙平行的边长为$(24 - 2x)$m。
由于墙长$8$m，所以$0＜24 - 2x\leq8$。
解不等式$24 - 2x＞0$，得$x＜12$；
解不等式$24 - 2x\leq8$，得$x\geq8$。
所以$x$的取值范围是$8\leq x＜12$。
养鸡场的面积$S = x(24 - 2x)=-2x^2 + 24x$。
对于二次函数$y = ax^2 + bx + c$（$a\neq0$），其对称轴为$x = -\frac{b}{2a}$，在函数$S = -2x^2 + 24x$中，$a = -2$，$b = 24$，所以对称轴为$x = -\frac{24}{2×(-2)} = 6$。
因为$a = -2＜0$，所以二次函数图象开口向下，在对称轴左侧$S$随$x$的增大而增大，在对称轴右侧$S$随$x$的增大而减小。
而$x$的取值范围是$8\leq x＜12$，在这个区间内$S$随$x$的增大而减小。
所以当$x = 8$时，$S$有最大值，$S=-2×8^2 + 24×8 = -128 + 192 = 64$（$m^2$）。
【答案】：$64$。

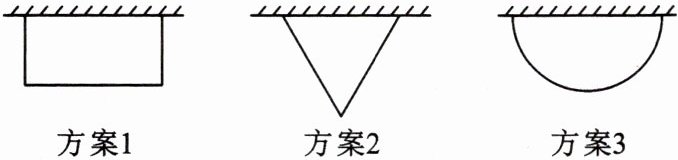
7.(自贡市中考)九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰三角形(底边靠墙)、半圆形这三种方案,最佳方案是(C)

A.方案1
B.方案2

C.方案3
D.方案1或方案2

答案： 【解析】：
本题需要根据三种方案分别计算出菜园的面积，再比较大小，从而得出最佳方案。
方案1：围成矩形
设垂直于墙的一边长为$x$米，则平行于墙的一边长为$(8 - 2x)$米。
根据矩形面积公式$S = 长×宽$，可得菜园面积$S_1 = x(8 - 2x)=-2x^2 + 8x$。
对于二次函数$y=ax^2+bx+c$（$a\neq0$），当$a\lt0$时，函数在$x = -\frac{b}{2a}$处取得最大值。
在$S_1 = -2x^2 + 8x$中，$a = -2$，$b = 8$，则$x = -\frac{8}{2×(-2)} = 2$。
将$x = 2$代入$S_1$可得$S_1 = -2×2^2 + 8×2 = 8$（平方米）。
方案2：围成等腰三角形（底边靠墙）
设等腰三角形的腰长为$x$米，则底边长为$(8 - 2x)$米。
根据等腰三角形面积公式$S=\frac{1}{2}×底×高$，需要先求出高。
根据勾股定理，高$h = \sqrt{x^2 - (\frac{8 - 2x}{2})^2}=\sqrt{x^2 - (4 - x)^2}=\sqrt{x^2 - 16 + 8x - x^2}=\sqrt{8x - 16}$。
则菜园面积$S_2 = \frac{1}{2}(8 - 2x)\sqrt{8x - 16}=(4 - x)\sqrt{8x - 16}$。
根据均值不等式$ab\leqslant(\frac{a+b}{2})^2$（$a,b\geqslant0$，当且仅当$a = b$时等号成立），
对于$(4 - x)\sqrt{8x - 16}$，令$a = 4 - x$，$b = \sqrt{8x - 16}$，
因为$(4 - x)+\frac{8x - 16}{8}=4 - x + x - 2 = 2$（定值），
当$4 - x=\frac{8x - 16}{8}$时，即$32 - 8x = 8x - 16$，$16x = 48$，$x = 3$时，$S_2$取得最大值。
此时底边长为$8 - 2×3 = 2$米，高为$\sqrt{3^2 - 1^2}=\sqrt{9 - 1}=2\sqrt{2}$米，$S_2 = \frac{1}{2}×2×2\sqrt{2}=2\sqrt{2}\approx2×1.414 = 2.828\lt 8$平方米。
方案3：围成半圆形
设半圆的半径为$r$米，则半圆的弧长为$8$米。
根据圆的弧长公式$l=\pi r$（$l$为弧长），可得$\pi r = 8$，则$r = \frac{8}{\pi}$。
根据圆的面积公式$S=\pi r^2$，可得半圆的面积$S_3 = \frac{1}{2}\pi r^2=\frac{1}{2}\pi(\frac{8}{\pi})^2=\frac{32}{\pi}\approx\frac{32}{3.14}\approx 10.19\gt 8$平方米。
比较$S_1$，$S_2$，$S_3$的大小，$S_3\gt S_1\gt S_2$，所以最佳方案是方案3。
【答案】：C