第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
7. 在矩形 ABCD 中,$AD= 8$,半径为 5 的$\odot O$与 BC 相切,且经过 A,D 两点,则$AB=$
2或8
.
答案:
2或8
8.(宜宾市中考)我国古代数学家赵爽的"弦图"是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如图所示),若直角三角形的内切圆半径为 3,小正方形的面积为 49,则大正方形的面积为
289
.
答案:
289
9. (陕西省中考)如图所示,正方形 ABCD 的边长为 4,$\odot O$的半径为 1,若$\odot O$在正方形 ABCD 内平移($\odot O$可以与该正方形的边相切),则点 A 到$\odot O$上的点的距离的最大值为
3$\sqrt{2}$+1
.
答案:
3$\sqrt{2}$+1
10. (教材第100页例2变式)如图,$\triangle ABC的内切圆\odot O$与 BC,CA,AB 分别相切于点 D,E,F,且$AB= 18cm,BC= 28cm,CA= 26cm$,求:
(1)AF,BD,CE 的长;
(2)若$\triangle ABC的面积为144cm^{2}$,求出内切圆的半径 r.

(1)AF,BD,CE 的长;
(2)若$\triangle ABC的面积为144cm^{2}$,求出内切圆的半径 r.

答案:
解:
(1)根据切线长定理得:AE = AF,BF = BD,CE = CD.设AF = AE = xcm,则CE = CD = (26 - x)cm,BF = BD = (18 - x)cm.
∵BC = 28cm,
∴(18 - x)+(26 - x)=28.解得x = 8.
∴AF = 8cm,BD = 10cm,CE = 18cm.
(2)连接OA,OB,OC,
∴S△ABC = S△ABO + S△BOC + S△AOC,即144 = $\frac{1}{2}$AB·r + $\frac{1}{2}$BC·r + $\frac{1}{2}$AC·r,
∴144 = $\frac{1}{2}$r(AB + BC + AC),
∴r = 4cm.
解:
(1)根据切线长定理得:AE = AF,BF = BD,CE = CD.设AF = AE = xcm,则CE = CD = (26 - x)cm,BF = BD = (18 - x)cm.
∵BC = 28cm,
∴(18 - x)+(26 - x)=28.解得x = 8.
∴AF = 8cm,BD = 10cm,CE = 18cm.
(2)连接OA,OB,OC,

∴S△ABC = S△ABO + S△BOC + S△AOC,即144 = $\frac{1}{2}$AB·r + $\frac{1}{2}$BC·r + $\frac{1}{2}$AC·r,
∴144 = $\frac{1}{2}$r(AB + BC + AC),
∴r = 4cm.
11. (核心素养·直观想象)(银川外国语实验学校模拟)如图,AB 是$\odot O$的直径,过点 A 作$\odot O$的切线 AC,点 P 是射线 AC 上的动点,连接 OP,过点 B 作$BD// OP$,交$\odot O$于点 D,连接 PD.
(1)求证:PD 是$\odot O$的切线;
(2)当四边形 POBD 是平行四边形时,求$∠APO$的度数.
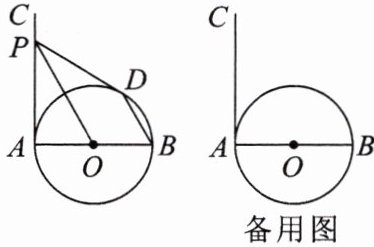
(1)求证:PD 是$\odot O$的切线;
(2)当四边形 POBD 是平行四边形时,求$∠APO$的度数.

答案:
(1)证明:连接OD.

∵PA切⊙O于A,
∴PA⊥AB,即∠PAO = 90°,
∵OP //BD,
∴∠DBO = ∠AOP,∠BDO = ∠DOP,
∵OD = OB,
∴∠BDO = ∠DBO,
∴∠DOP = ∠AOP,在△AOP和△DOP中,$\begin{cases}AO = DO\\\angle AOP = \angle DOP\\PO = PO\end{cases}$(SAS),
∴∠PDO = ∠PAO = 90°,即OD⊥PD,
∵OD是⊙O的半径,
∴PD是⊙O 的切线.
(2)解:如图,连接OD.由
(1)知:△AOP≌△DOP,
∴PA = PD.
∵四边形POBD是平行四边形,
∴PD = OB.
∵OB = OA,
∴PA = OA,
∴∠APO = ∠AOP.
∵∠PAO = 90°,
∴∠APO = ∠AOP = 45°.
(1)证明:连接OD.


∵PA切⊙O于A,
∴PA⊥AB,即∠PAO = 90°,
∵OP //BD,
∴∠DBO = ∠AOP,∠BDO = ∠DOP,
∵OD = OB,
∴∠BDO = ∠DBO,
∴∠DOP = ∠AOP,在△AOP和△DOP中,$\begin{cases}AO = DO\\\angle AOP = \angle DOP\\PO = PO\end{cases}$(SAS),
∴∠PDO = ∠PAO = 90°,即OD⊥PD,
∵OD是⊙O的半径,
∴PD是⊙O 的切线.
(2)解:如图,连接OD.由
(1)知:△AOP≌△DOP,
∴PA = PD.
∵四边形POBD是平行四边形,
∴PD = OB.
∵OB = OA,
∴PA = OA,
∴∠APO = ∠AOP.
∵∠PAO = 90°,
∴∠APO = ∠AOP = 45°.
查看更多完整答案,请扫码查看


