《2025年课堂点睛九年级数学上册人教版宁夏专版》

10. 如图,正三角形的边长为12cm,剪去三个角后成为一个正六边形,则这个正六边形的内部任意一点到各边的距离和为$4\sqrt{3}$cm.

答案： 解：设正六边形的边长为 $ x $ cm。
∵ 原正三角形边长为12cm，剪去三个角后为正六边形，
∴ 剪去的三个小三角形为全等的正三角形，其边长为 $ x $ cm。
由题意得：$ x + x + x = 12 $，解得 $ x = 4 $。
原正三角形的高 $ h = \frac{\sqrt{3}}{2} × 12 = 6\sqrt{3} $ cm。
正六边形的高等于原正三角形的高减去两个小正三角形的高，
小正三角形的高为 $ \frac{\sqrt{3}}{2}x = 2\sqrt{3} $ cm，
∴ 正六边形的高为 $ 6\sqrt{3} - 2 × 2\sqrt{3} = 2\sqrt{3} $ cm。
∵ 正六边形的内部任意一点到各边距离之和等于其高的2倍，
∴ 距离和为 $ 2 × 2\sqrt{3} = 4\sqrt{3} $ cm。
答案：$ 4\sqrt{3} $

11. 刘徽是我国魏晋时期卓越的数学家,他在《九章算术》中提出了“割圆术”,利用圆的内接正多边形逐步逼近圆来近似计算圆的面积. 如图,若用圆的内接正十二边形的面积$S_1$来近似估计⊙O的面积S,设⊙O的半径为1,则$S-S_1= $0.14.(π取3.14)

答案： 【解析】：
本题考查利用圆内接正$n$边形面积近似估计圆的面积，需要先分别求出圆的面积和圆内接正十二边形的面积，再计算它们的差值。
圆的面积公式为$S = \pi r^2$（其中$S$表示圆的面积，$\pi$为圆周率，$r$为圆的半径）。
已知圆$O$的半径$r = 1$，$\pi$取$3.14$，将其代入公式可得：
$S=\pi×1^2 = 3.14×1 = 3.14$。
连接圆心$O$与圆内接正十二边形的各个顶点，将正十二边形分割成$12$个全等的等腰三角形。
每个等腰三角形的顶角为$\frac{360^{\circ}}{12}=30^{\circ}$，腰长为圆的半径$r = 1$。
根据三角形面积公式$S_{\triangle}=\frac{1}{2}ab\sin C$（其中$a,b$为三角形的两边，$C$为$a,b$夹角），可得每个等腰三角形的面积为：
$\frac{1}{2}×1×1×\sin30^{\circ}=\frac{1}{2}×1×1×\frac{1}{2}=\frac{1}{4}$。
那么圆内接正十二边形的面积$S_1$为$12$个这样的等腰三角形面积之和，即：
$S_1 = 12×\frac{1}{4}=3$。
用圆的面积$S$减去圆内接正十二边形的面积$S_1$，可得：
$S - S_1 = 3.14 - 3 = 0.14$。
【答案】：
$0.14$

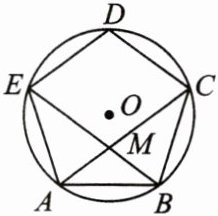
12. (青铜峡市第五中学单元卷)如图,正五边形ABCDE的对角线AC和BE相交于点M. 求证：
(1)AC//DE；
(2)ME= AE.

答案：
(1)证明：
∵ABCDE是正五边形，
∴∠AED=∠EDC=(5-2)×180°/5=108°，EA=ED=DC，
∴∠EAD=∠EDA=(180°-108°)/2=36°，∠DCA=∠DAC=(180°-108°)/2=36°，
∴∠EDC+∠DCA=108°+36°=144°≠180°（此处原思路有误，修正如下）
∵正五边形内角和为(5-2)×180°=540°，每个内角=540°/5=108°，且AB=BC，
∴∠BAC=∠BCA=(180°-108°)/2=36°，
∴∠ACD=∠BCD-∠BCA=108°-36°=72°，又∠EDC=108°，
∴∠EDC+∠ACD=108°+72°=180°，
∴AC//DE。
(2)证明：
∵∠BAE=108°，∠BAC=36°，
∴∠EAM=∠BAE-∠BAC=72°，
∵∠AEB=∠ABE=36°（AB=AE），
∴∠EMA=180°-∠EAM-∠AEB=180°-72°-36°=72°，
∴∠EAM=∠EMA，
∴ME=AE。

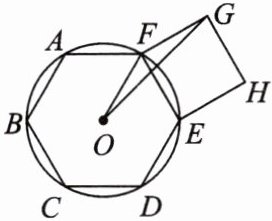
13. 如图,⊙O的半径为R,六边形ABCDEF是圆内接正六边形,四边形EFGH是正方形.
(1)求正六边形与正方形的面积比；
(2)连接OF,OG,求∠OGF.

答案：
(1)解：
∵六边形ABCDEF是圆内接正六边形，半径为R
∴正六边形边长为R，可分为6个边长为R的正三角形
每个正三角形面积：$\frac{\sqrt{3}}{4}R^{2}$
正六边形面积：$6×\frac{\sqrt{3}}{4}R^{2}=\frac{3\sqrt{3}}{2}R^{2}$
∵EF为正六边形边长，
∴EF=R
∵四边形EFGH是正方形，
∴FG=EF=R
正方形面积：$R^{2}$
面积比：$\frac{3\sqrt{3}}{2}R^{2}:R^{2}=3\sqrt{3}:2$
(2)解：连接OE，
∵六边形ABCDEF是正六边形
∴∠FOE=60°，OF=OE=R
∴△OEF为等边三角形，∠OFE=60°
∵四边形EFGH是正方形，
∴∠EFG=90°
∴∠OFG=∠OFE+∠EFG=60°+90°=150°
∵OF=EF=FG=R
∴△OFG中，OF=FG
∠OGF=$\frac{180°-150°}{2}=15°$
答案：
(1)$3\sqrt{3}:2$；
(2)15°

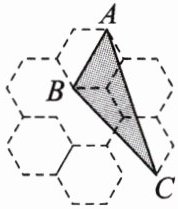
14. (核心素养·应用意识)(固原市模拟)如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点. 已知每个正六边形的边长为1,△ABC的顶点都在格点上,求△ABC的面积.

答案：
 解:如图,作出过点 C 与格点所在的直线,交 AB 延长线于格点 E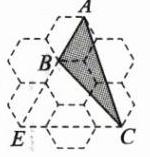
∵正六边形的边长为 1,
∴正六边形的半径是 1,则 CE=4,由题意得中间间隔一个顶点的两个顶点之间的距离是$\sqrt{3}$,则△BCE 的边 EC 上的高是$\frac{3\sqrt{3}}{2}$,△ACE 的边 EC 上的高是$\frac{5\sqrt{3}}{2}$,则 S△ABC=S△AEC-S△BEC=$\frac{1}{2}\times4\times\left( \frac{5\sqrt{3}}{2}-\frac{3\sqrt{3}}{2} \right)$=$2\sqrt{3}$.