《2025年课堂点睛九年级数学上册人教版宁夏专版》

1.(西安市高新一中月考)我国古代数学著作《增删算法统宗》记载"圆中方形"问题:"今有圆田一段,中间有个方池,丈量田地待耕犁,恰好三分在记,池面至周有数,每边三步无疑,内方圆径若能知,堪作算中第一."其大意为:如图,有一块圆形的田,中间有一块正方形水池,测量出除水池外圆内可耕地的面积恰好为72平方步,从水池边到圆周,每边相距3步远.如果你能求出正方形的边长和圆的直径,那么你的运算能力就数第一了.若设正方形的边长是x步,则列出的方程是(B)

A.$\pi(x+3)^{2}-x^{2}= 72$
B.$\pi(\frac{x}{2}+3)^{2}-x^{2}= 72$
C.$\pi(x+3)^{2}-x^{2}= 36$
D.$\pi(\frac{x}{2}+3)^{2}-x^{2}= 36$

答案： B

2.《九章算术》中记载了一个数学问题:"今有户高多于广六尺八寸,两隅相去适一丈,问户高、广各几何?"译文为:"已知有一扇矩形门的高比宽多6尺8寸,门的对角线长1丈(1丈= 10尺,1尺= 10寸),那么门的高和宽各是多少?"若设门的宽为x尺,则可列方程：$x^{2}+(x+6.8)^{2}=10^{2}$.

答案： $x^{2}+(x+6.8)^{2}=10^{2}$

3.《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:"直田积八百六十四步,只云长阔共六十步,问长多阔几何".意思是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多多少步? 根据题意得,长比宽多12步.

答案： 12

4.(宁夏自治区中考)你知道吗,对于一元二次方程,我国古代数学家还研究过其几何解法呢？以方程$x^{2}+5x-14= 0即x(x+5)= 14$为例加以说明.数学家赵爽(公元3～4世纪)在其所著的《勾股圆方图注》中记载的方法是:构造图(如下面左图)中大正方形的面积是$(x+x+5)^{2}$,其中它又等于四个矩形的面积加上中间小正方形的面积,即$4×14+5^{2}$,据此易得$x= 2$.那么在下面右边三个构图(矩形的顶点均落在边长为1的小正方形网格格点上)中,能够说明方程$x^{2}-4x-12= 0$的正确构图是______.(只填序号)

②

答案： ②

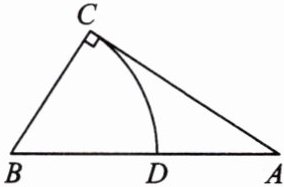
5.(银川景博学校月考)古希腊数学家丢番图(公元250年前后)在《算术》中就提到了一元二次方程的问题,不过当时古希腊人还没有寻求到它的求根公式,只能用图解等方法来求解,在欧几里得的《几何原本》中,形如$x^{2}+ax= b^{2}(a＞0,b＞0)$的方程的图解法是：如图,以$\frac{a}{2}$和b为两直角边作$\text{Rt}\triangle ABC$,再在斜边上截取$BD= \frac{a}{2}$,则AD的长就是所求方程的解.
(1)请用含字母a、b的代数式表示AD的长；
(2)请利用你已学的知识说明该图解法的正确性,并说说这种解法的遗憾之处.

答案： 解:
(1)$\because \angle C=90^{\circ },BC=\frac {a}{2},AC$$=b,\therefore AB=\sqrt {b^{2}+\frac {a^{2}}{4}},\therefore AD=\sqrt {b^{2}+\frac {a^{2}}{4}}-\frac {a}{2}=\frac {\sqrt {4b^{2}+a^{2}}-a}{2}$.
(2)用求根公式求得:$x_{1}=\frac {-\sqrt {4b^{2}+a^{2}}-a}{2},x_{2}=\frac {\sqrt {4b^{2}+a^{2}}-a}{2}$.正确性:AD 的长就是方程的正根.遗憾之处:图解法不能表示方程的负根.