《2025年课堂点睛九年级数学上册人教版宁夏专版》

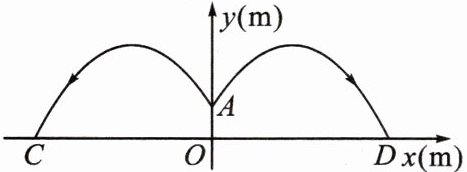
6. 某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同,如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为$y= -\frac{1}{6}(x-5)^{2}+6$.
(1)求雕塑高OA；
(2)求落水点C,D之间的距离；
(3)若需要在OD上的点E处竖立雕塑EF,OE= 10m,EF= 1.8m,EF⊥OD. 问：顶部F是否会碰到水柱？请通过计算说明.

答案： 解:
(1)当$x=0$时,$y=-\dfrac{1}{6}(0-5)^{2}+6=\dfrac{11}{6}$,$\therefore$点$A$的坐标为$\left(0,\dfrac{11}{6}\right)$,$\therefore$雕塑高$\dfrac{11}{6}\ \text{m}$.
(2)当$y=0$时,$-\dfrac{1}{6}(x-5)^{2}+6=0$.解得$x_{1}=-1$(舍去),$x_{2}=11$,$\therefore$点$D$的坐标为$(11,0)$,$\therefore OD=11\text{m}$.$\because$从$A$点向四周喷水,喷出的水柱为抛物线,且形状相同,$\therefore OC=OD=11\text{m}$,$\therefore CD=OC+OD=22\text{m}$.
(3)当$x=10$时,$y=-\dfrac{1}{6}(10-5)^{2}+6=\dfrac{11}{6}$,$\therefore$点$\left(10,\dfrac{11}{6}\right)$在抛物线$y=-\dfrac{1}{6}(x-5)^{2}+6$上.又$\because \dfrac{11}{6}\approx1.83＞1.8$,$\therefore$顶部$F$不会碰到水柱.

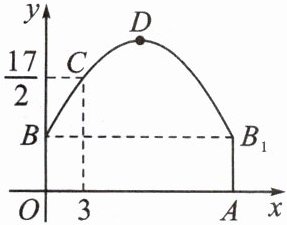
7. (核心素养·应用意识)(咸阳市启迪中学期中)如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m,按照图中所示的直角坐标系,抛物线可以用$y= -\frac{1}{6}x^{2}+bx+c$表示,且抛物线上的点C到墙面OB的水平距离为3m时,到地面OA的距离为$\frac{17}{2}m$.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离；
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过？
(3)在抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米？

答案： 解:
(1)把$B(0,4)$,$C\left(3,\dfrac{17}{2}\right)$代入函数关系式$y=-\dfrac{1}{6}x^{2}+bx+c$得$\begin{cases} c=4, \\ -\dfrac{1}{6}×3^{2}+3b+c=\dfrac{17}{2}, \end{cases}$解得$\begin{cases} b=2, \\ c=4, \end{cases}$所以抛物线解析式为$y=-\dfrac{1}{6}x^{2}+2x+4$,则$y=-\dfrac{1}{6}(x-6)^{2}+10$,所以$D(6,10)$,所以拱顶$D$到地面$OA$的距离为$10\text{m}$.
(2)由题意得,当货运汽车最外侧与地面$OA$的交点为$(2,0)$或$(10,0)$,即当$x=2$或$x=10$时,$y=\dfrac{22}{3}＞6$,所以这辆货车能安全通过.
(3)令$y=8$,则$-\dfrac{1}{6}(x-6)^{2}+10=8$,解得$x_{1}=6+2\sqrt{3}$,$x_{2}=6-2\sqrt{3}$,则$x_{1}-x_{2}=4\sqrt{3}$,所以两排灯的水平距离最小是$4\sqrt{3}\ \text{m}$.