第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
方法指导
(1)条件:如图,在等腰△ABC中,AB= BC,∠DBE= 1/2∠CBA.
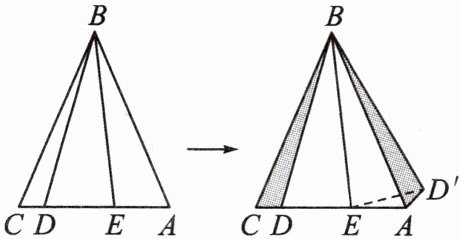
结论:△DBE≌______.
(1)条件:如图,在等腰△ABC中,AB= BC,∠DBE= 1/2∠CBA.

结论:△DBE≌______.
答案:
△D'BE
(2)条件:如图,在等腰Rt△ABC中,∠MAN= 45°.
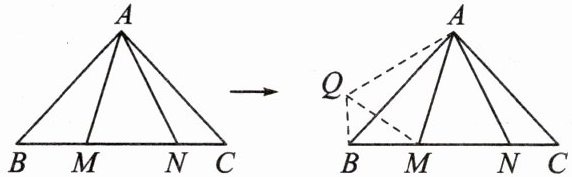
结论$:①MN= ______;②CN^2+BM^2= ______.$

结论$:①MN= ______;②CN^2+BM^2= ______.$
答案:
①MQ;②MN²
(3)条件:如图,在正方形ABCD中,∠EAF= 45°.
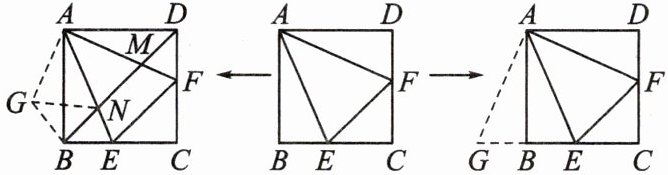
结论:①EF= DF+______;②△CEF的周长等于正方形ABCD周长的一半$;③DM^2+BN^2= ______.$

结论:①EF= DF+______;②△CEF的周长等于正方形ABCD周长的一半$;③DM^2+BN^2= ______.$
答案:
①BE;③MN²
1. 如图,在△ABC中,∠BAC= 90°,AB= AC,D,E在BC上,∠DAE= 45°,为了探究BD,DE,CE之间的等量关系,现将△AEC绕A顺时针旋转90°后成△AFB,连接DF,经探究,你所得到的BD,DE,CE之间的等量关系式是
BD²+CE²=DE²
.(无须证明)
答案:
BD²+CE²=DE²
2. 如图,在△ABC中,∠BAC= 120°,AB= AC,D,E在BC上,∠DAE= 60°,∠ADE= 45°,试仿照(1)的方法,利用图形的旋转变换,探究BD,DE,CE之间的等量关系,并证明你的结论.
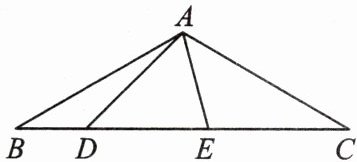

答案:
CE²=BD²+DE².证明:将△AEC绕A顺时针旋转120°后成△AFB,连接DF;在△ABC中,∠BAC=120°,AB=AC,
∴∠ABD=∠ACE=30°,由旋转的性质可知,△AEC≌△AFB,
∴∠ABF=∠ACE =30°,FB=CE.
∴∠FBD=∠ABF+∠ABD=60°,∠FAE=120°.又∠DAE=60°,故∠FAD=∠FAE−∠DAE=60°,易证△AFD≌△AED,故FD=DE.
∵∠ADE=45°,
∴∠ADF=45°,故∠BDF=90°.在Rt△BDF中,由勾股定理,得BF²=BD²+DF²,
∴CE²=BD²+DE².
∴∠ABD=∠ACE=30°,由旋转的性质可知,△AEC≌△AFB,
∴∠ABF=∠ACE =30°,FB=CE.
∴∠FBD=∠ABF+∠ABD=60°,∠FAE=120°.又∠DAE=60°,故∠FAD=∠FAE−∠DAE=60°,易证△AFD≌△AED,故FD=DE.
∵∠ADE=45°,
∴∠ADF=45°,故∠BDF=90°.在Rt△BDF中,由勾股定理,得BF²=BD²+DF²,
∴CE²=BD²+DE².
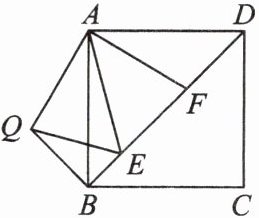
3. 如图,在正方形ABCD中,E,F是对角线BD上的两点,且∠EAF= 45°,将△ADF绕点A顺时针旋转90°,得到△ABQ,连接EQ.求证:
(1)EA是∠QED的平分线;
$(2)EF^2= BE^2+DF^2.$
(1)EA是∠QED的平分线;
$(2)EF^2= BE^2+DF^2.$

答案:
(1)由旋转的性质,得AQ=AF,∠QAF=90°.
∵∠EAF=45°,
∴∠QAE=∠QAF−∠EAF=45°,
∴∠QAE=∠FAE.在△AQE和△AFE中,{AQ=AF,∠QAE=∠FAE,AE=AE},
∴△AQE≌△AFE(SAS),
∴∠AEQ=∠AEF,
∴EA是∠QED的平分线.
(2)由
(1)知△AQE≌△AFE,
∴QE=FE.由旋转的性质,得QB=DF,∠ABQ=∠ADF=45°=∠ABD,
∴∠QBE=90°.在Rt△QBE中,QB²+BE²=QE²,
∴EF²=BE²+DF².
(1)由旋转的性质,得AQ=AF,∠QAF=90°.
∵∠EAF=45°,
∴∠QAE=∠QAF−∠EAF=45°,
∴∠QAE=∠FAE.在△AQE和△AFE中,{AQ=AF,∠QAE=∠FAE,AE=AE},
∴△AQE≌△AFE(SAS),
∴∠AEQ=∠AEF,
∴EA是∠QED的平分线.
(2)由
(1)知△AQE≌△AFE,
∴QE=FE.由旋转的性质,得QB=DF,∠ABQ=∠ADF=45°=∠ABD,
∴∠QBE=90°.在Rt△QBE中,QB²+BE²=QE²,
∴EF²=BE²+DF².
查看更多完整答案,请扫码查看


