《2025年南通小题课时作业本八年级数学上册苏科版》

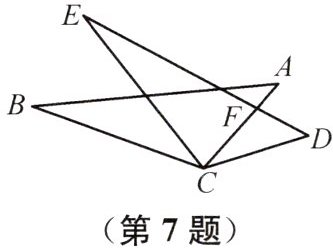
7 如图,已知$\triangle ABC \cong \triangle DEC$,$\angle ACB=100^{\circ}$,$\angle D=35^{\circ}$,则$\angle E$的度数为 (B)
A. $35^{\circ}$
B. $45^{\circ}$
C. $55^{\circ}$
D. 无法计算
!
!
!
!

答案： B

8 如图,点$E$在$AB$上,$AC$与$DE$相交于点$F$,$\triangle ABC \cong \triangle DEC$,$\angle A=20^{\circ}$,$\angle B=\angle CEB=65^{\circ}$,则$\angle DFA$的度数为 (B)
A. $65^{\circ}$
B. $70^{\circ}$
C. $85^{\circ}$
D. $110^{\circ}$

答案： B

9 如图,在$\triangle ABC$中,$AD \perp BC$于点$D$,$BE \perp AC$于点$E$,$AD$与$BE$相交于点$F$,$\triangle ADC \cong \triangle BDF$,若$BD=4$,$DC=2$,则$\triangle ABC$的面积为12.

答案： 12

10 (2025 宜兴月考)如图,$\triangle AOB \cong \triangle ADC$,$\angle O=90^{\circ}$,若$\angle OAD=\alpha$,$\angle ABO=\beta$. 当$BC // OA$时,$\alpha$与$\beta$之间的数量关系为$\alpha = 2\beta$.

答案： $ \alpha = 2\beta $

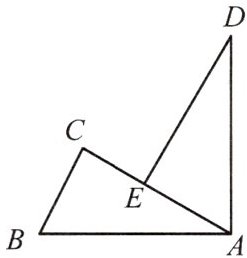
11 如图,$A,E,C$三点在同一直线上,且$\triangle ABC \cong \triangle DAE$.
(1) 线段$DE,CE,BC$有怎样的数量关系? 请说明理由;
(2) 请你猜想$\triangle ADE$满足什么条件时,$DE // BC$,并说明理由.
!

答案：
(1) $ DE = CE + BC $。理由如下：
因为 $ \triangle ABC \cong \triangle DAE $，
所以 $ AE = BC $，$ DE = AC $。
因为 $ A $，$ E $，$ C $ 三点在同一直线上，
所以 $ AC = AE + CE $，
所以 $ DE = CE + BC $。
(2) 当 $ \triangle ADE $ 满足 $ \angle AED = 90^{\circ} $ 时，$ DE // BC $。理由如下：因为 $ \triangle ABC \cong \triangle DAE $，$ \angle AED = 90^{\circ} $，
所以 $ \angle C = \angle AED = 90^{\circ} $，$ \angle DEC = 180^{\circ} - \angle AED = 90^{\circ} $，所以 $ \angle C = \angle DEC $，
所以 $ DE // BC $，
即当 $ \triangle ADE $ 满足 $ \angle AED = 90^{\circ} $ 时，$ DE // BC $。

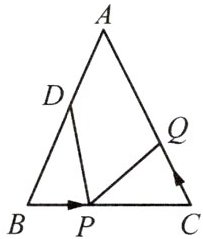
12 新考法 (2025 广陵月考)如图,在$\triangle ABC$中,$AB=AC=24\mathrm{~cm}$,$BC=16\mathrm{~cm}$,$D$为$AB$的中点. 如果点$P$在线段$BC$上以$4\mathrm{~cm}/\mathrm{s}$的速度由点$B$向点$C$运动. 同时,点$Q$在线段$CA$上以$a\mathrm{~cm}/\mathrm{s}$的速度由点$C$向$A$点运动,设运动的时间为$t\mathrm{~s}$.
(1) ①$BP=$4t$\mathrm{cm}$;②$CP=$16 - 4t$\mathrm{cm}$;③$CQ=$at$\mathrm{cm}$;(用含$t,a$的式子表示)
(2) 若以$D,B,P$为顶点的三角形和以$P,C,Q$为顶点的三角形全等,求$a,t$的值.$\begin{cases}a = 4\\t = 1\end{cases}$或$\begin{cases}a = 6\\t = 2\end{cases}$
!

答案： 【解析】：
### $(1)$ 求$BP$、$CP$、$CQ$的表达式
根据路程$=$速度$×$时间，已知点$P$的速度是$4cm/s$，运动时间为$t s$，所以$BP = 4t cm$。
因为$BC = 16cm$，$BP = 4t cm$，所以$CP=BC - BP=(16 - 4t)cm$。
已知点$Q$的速度是$a cm/s$，运动时间为$t s$，所以$CQ = at cm$。
### $(2)$ 求$a$，$t$的值
已知$AB = AC = 24cm$，$D$为$AB$的中点，则$BD=\frac{1}{2}AB = 12cm$。
因为$\triangle DBP$和$\triangle PCQ$全等，分两种情况讨论：
**情况一：当$\triangle DBP\cong\triangle PCQ$时**
根据全等三角形对应边相等可得$\begin{cases}BD = PC\\BP = CQ\end{cases}$，即$\begin{cases}12 = 16 - 4t\\4t = at\end{cases}$。
解$12 = 16 - 4t$：
移项可得$4t=16 - 12$，即$4t = 4$，解得$t = 1$。
把$t = 1$代入$4t = at$：
得到$4×1=a×1$，解得$a = 4$。
**情况二：当$\triangle DBP\cong\triangle QCP$时**
根据全等三角形对应边相等可得$\begin{cases}BD = CQ\\BP = PC\end{cases}$，即$\begin{cases}12 = at\\4t = 16 - 4t\end{cases}$。
解$4t = 16 - 4t$：
移项可得$4t+4t = 16$，即$8t = 16$，解得$t = 2$。
把$t = 2$代入$12 = at$：
得到$12=a×2$，解得$a = 6$。
综上，$\begin{cases}a = 4\\t = 1\end{cases}$或$\begin{cases}a = 6\\t = 2\end{cases}$。
【答案】：
$(1)$ ①$\boldsymbol{4t}$；②$\boldsymbol{16 - 4t}$；③$\boldsymbol{at}$
$(2)$$\boldsymbol{\begin{cases}a = 4\\t = 1\end{cases}}$或$\boldsymbol{\begin{cases}a = 6\\t = 2\end{cases}}$