《2025年南通小题课时作业本八年级数学上册苏科版》

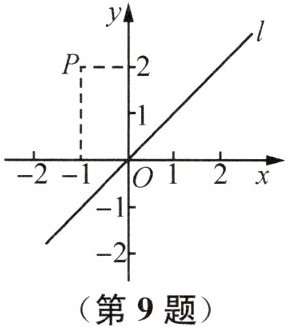
9 如图,将点$P(-1,2)$关于第一、三象限的角平分线l对称,得到点$P'$,则点$P'$的坐标为 (B)
A.$(2,1)$ B.$(2,-1)$ C.$(1,-2)$ D.$(-1,-2)$
!

答案： B

10 (学科融合)如图,从点$M(0,3)$发出一束光,经x轴反射,过点$N(6,5)$,则这束光从点M到点N所经过的路径的长为 (C)
A.8
B.9
C.10
D.12.5

答案： C

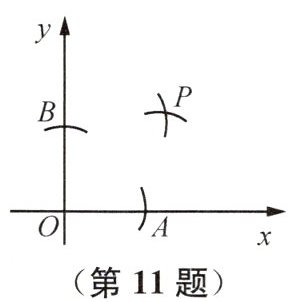
11 (2025连云港灌云月考)如图,点A,B分别在x轴,y轴上,$OA=OB$,分别以点A,B为圆心,以大于$\frac {1}{2}AB$长为半径画弧,两弧交于点P.若点P的坐标为$(2a,3a-4)$,则a的值为4.

答案： 4

12 (2025无锡梁溪月考)如图,过点A的直线$l// x$轴,点B在x轴的正半轴上,OC平分$∠AOB$交直线l于点$C(2,4)$,则点A的坐标是$(-3,4)$.

答案： $(-3,4)$

13 在平面直角坐标系中,点$A(a,b),B(2,2)$,且$|a-b+8|+\sqrt {3a+2b-6}=0$.
(1)求点A的坐标;
(2)过点A作$AC⊥x$轴于点C,连接BC,AB,求$\triangle ABC$的面积;
(3)在(2)的条件下,延长AB交x轴于点D,AB交y轴于点E,则OD与OE是否相等?请说明理由.

答案：
解:
(1) 由 $|a - b + 8| + \sqrt{3a + 2b - 6} = 0$,
得 $\begin{cases}a - b + 8 = 0\\3a + 2b - 6 = 0\end{cases}$, 解得 $\begin{cases}a = -2\\b = 6\end{cases}$,
所以点 $A$ 的坐标为 $(-2,6)$.
(2) 如图1, 过点 $B$ 作 $BF \perp x$ 轴于点 $F$,
则 $S_{\triangle ABC} = S_{梯形ACFB} - S_{\triangle BCF} = \frac{1}{2} × (2 + 6) × 4 - \frac{1}{2} × 4 × 2 = 12$.
(3) $OD$ 与 $OE$ 相等. 理由如下:
如图2, 设点 $D$ 的坐标为 $(x,0)(x ＞ 0)$, 点 $E$ 的坐标为 $(0,y)(y ＞ 0)$,
则 $CD = x + 2$, $OE = y$.
因为 $S_{\triangle ABC} = S_{\triangle ACD} - S_{\triangle BCD}$,
所以 $12 = \frac{1}{2} × (x + 2) × 6 - \frac{1}{2} × (x + 2) × 2 = 2(x + 2)$,
解得 $x = 4$, 即 $OD = 4$.
又因为 $S_{\triangle BDE} = S_{\triangle ACD} - S_{梯形ACOE}$,
所以 $\frac{1}{2} × 4 × y = \frac{1}{2} × 6 × 6 - \frac{1}{2} × (y + 6) × 2$,
解得 $y = 4$, 即 $OE = 4$,
所以 $OD = OE$.

14 (2025宿迁宿城期末)在平面直角坐标系中,已知点M的坐标为$(2-t,2t)$,将点M到x轴的距离记作$d_{1}$,到y轴的距离记作$d_{2}$.
(1)若$t=3$,则$d_{1}+d_{2}=$7;
(2)若$t＜0,d_{1}=d_{2}$,求点M的坐标;
解: 由题意, 得 $d_1 = |2t|$, $d_2 = |2 - t|$.
因为 $t ＜ 0$,
所以 $2 - t ＞ 0$, $2t ＜ 0$,
所以 $d_1 = |2t| = -2t$, $d_2 = |2 - t| = 2 - t$,
因为 $d_1 = d_2$,
所以 $-2t = 2 - t$,
解得 $t = -2$,
所以 $2 - t = 2 - (-2) = 4$, $2t = 2 × (-2) = -4$,
所以点 $M$ 的坐标为 $(4,-4)$.
(3)若点M在第二象限,且$md_{1}-5d_{2}=10$(m为常数),求m的值.
解: 因为点 $M$ 在第二象限,
所以 $2 - t ＜ 0$, $2t ＞ 0$,
所以 $d_1 = |2t| = 2t$, $d_2 = |2 - t| = t - 2$.
因为 $md_1 - 5d_2 = 10$,
所以 $m × 2t - 5 × (t - 2) = 10$,
解得 $m = \frac{5}{2}$.

答案： 解:
(1) 7
(2) 由题意, 得 $d_1 = |2t|$, $d_2 = |2 - t|$.
因为 $t ＜ 0$,
所以 $2 - t ＞ 0$, $2t ＜ 0$,
所以 $d_1 = |2t| = -2t$, $d_2 = |2 - t| = 2 - t$,
因为 $d_1 = d_2$,
所以 $-2t = 2 - t$,
解得 $t = -2$,
所以 $2 - t = 2 - (-2) = 4$, $2t = 2 × (-2) = -4$,
所以点 $M$ 的坐标为 $(4,-4)$.
(3) 因为点 $M$ 在第二象限,
所以 $2 - t ＜ 0$, $2t ＞ 0$,
所以 $d_1 = |2t| = 2t$, $d_2 = |2 - t| = t - 2$.
因为 $md_1 - 5d_2 = 10$,
所以 $m × 2t - 5 × (t - 2) = 10$,
解得 $m = \frac{5}{2}$.