第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
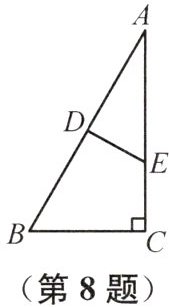
8 (2025常州溧阳期末)如图,在$△ABC$中,$∠C=90^{\circ }$,AB的垂直平分线分别交AB,AC于点D,E,若$BC=\sqrt {5}$,$AE:EC=3:2$,则AB的长为 (
A. $\sqrt {41}$
B. $\sqrt {30}$
C. $\sqrt {10}$
D. 3
!
!
!
!
B
)A. $\sqrt {41}$
B. $\sqrt {30}$
C. $\sqrt {10}$
D. 3
!
!
!
!

答案:
B
9 (2024南通启东月考)如图,在$Rt△ABC$中,分别以这个三角形的三边为边长向外侧作正方形,面积分别记为$S_{1}$,$S_{2}$,$S_{3}$。若$S_{3}+S_{2}-S_{1}=18$,则图中阴影部分的面积为 (
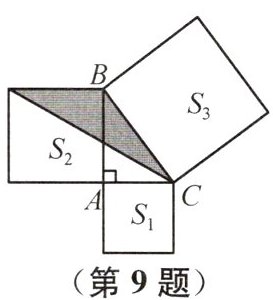
A. 6
B. $\frac {9}{2}$
C. 5
D. $\frac {7}{2}$
B
)
A. 6
B. $\frac {9}{2}$
C. 5
D. $\frac {7}{2}$
答案:
B
10 如图,在$△ABC$中,$∠C=90^{\circ }$,$c=2$,则$a^{2}+b^{2}+c^{2}=$
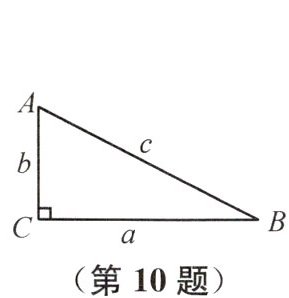
8
。
答案:
8
11 (2025徐州睢宁期中)对角线互相垂直的四边形叫作“垂美”四边形。现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O。若$AD=4$,$BC=2$,则$AB^{2}+CD^{2}=$
20
。
答案:
20
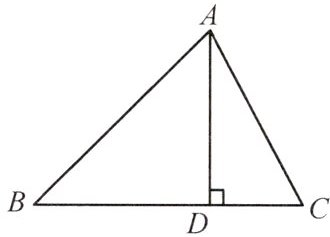
12 如图,在$△ABC$中,$AB=15$,$BC=14$,$AC=13$,求$△ABC$的面积。
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程。
作$AD⊥BC$,垂足为D,设$BD=x$,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积。
!
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程。
作$AD⊥BC$,垂足为D,设$BD=x$,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积。
!

答案:
解:在 $\triangle ABC$ 中,$AB=15$,$BC=14$,$AC=13$,
设 $BD=x$,则有 $CD=14-x$。
由勾股定理,得 $AD^{2}=AB^{2}-BD^{2}=15^{2}-x^{2}$,$AD^{2}=AC^{2}-CD^{2}=13^{2}-(14-x)^{2}$,
所以 $15^{2}-x^{2}=13^{2}-(14-x)^{2}$,
解得 $x=9$,
所以 $AD=12$,
所以 $S_{\triangle ABC}=\frac{1}{2}BC \cdot AD=\frac{1}{2} × 14 × 12=84$。
设 $BD=x$,则有 $CD=14-x$。
由勾股定理,得 $AD^{2}=AB^{2}-BD^{2}=15^{2}-x^{2}$,$AD^{2}=AC^{2}-CD^{2}=13^{2}-(14-x)^{2}$,
所以 $15^{2}-x^{2}=13^{2}-(14-x)^{2}$,
解得 $x=9$,
所以 $AD=12$,
所以 $S_{\triangle ABC}=\frac{1}{2}BC \cdot AD=\frac{1}{2} × 14 × 12=84$。
13 新考法 如图,在$Rt△ABC$中,$∠C=90^{\circ }$,$AB=10cm$,$AC=6cm$,动点P从点B出发沿射线BC以2cm/s的速度移动,设运动的时间为t s。
(1) 求边BC的长;
(2) 当$△ABP$为直角三角形时,求t的值;
(3) 当$△ABP$为等腰三角形时,求t的值。
!
!
!
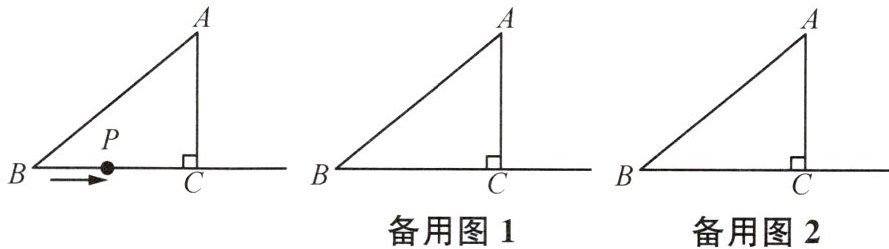
(1) 求边BC的长;
(2) 当$△ABP$为直角三角形时,求t的值;
(3) 当$△ABP$为等腰三角形时,求t的值。
!
!
!

答案:
解:
(1) 在 $Rt\triangle ABC$ 中,$BC^{2}=AB^{2}-AC^{2}=10^{2}-6^{2}=64$,所以 $BC=8\ cm$。
(2) 由题意可知 $BP=2t\ cm$。
①当 $\angle APB$ 为直角时,点 $P$ 与点 $C$ 重合,$BP=BC=8\ cm$,即 $t=4$;
②当 $\angle BAP$ 为直角时,$BP=2t\ cm$,$CP=(2t-8)\ cm$,$AC=6\ cm$,
在 $Rt\triangle ACP$ 中,$AP^{2}=6^{2}+(2t-8)^{2}$,
在 $Rt\triangle BAP$ 中,$AB^{2}+AP^{2}=BP^{2}$,即 $10^{2}+[6^{2}+(2t-8)^{2}]=(2t)^{2}$,
解得 $t=\frac{25}{4}$。
综上,当 $\triangle ABP$ 为直角三角形时,$t$ 的值为 4 或 $\frac{25}{4}$。
(3) ①当 $AB=BP$ 时,易得 $t=5$;
②当 $AB=AP$ 时,$BP=2BC=16\ cm$,易得 $t=8$;
③当 $BP=AP$ 时,$AP=BP=2t\ cm$,$CP=|2t-8|\ cm$,$AC=6\ cm$。
在 $Rt\triangle ACP$ 中,$AP^{2}=AC^{2}+CP^{2}$,即 $(2t)^{2}=6^{2}+(2t-8)^{2}$,解得 $t=\frac{25}{8}$。
综上,当 $\triangle ABP$ 为等腰三角形时,$t$ 的值为 5 或 8 或 $\frac{25}{8}$。
(1) 在 $Rt\triangle ABC$ 中,$BC^{2}=AB^{2}-AC^{2}=10^{2}-6^{2}=64$,所以 $BC=8\ cm$。
(2) 由题意可知 $BP=2t\ cm$。
①当 $\angle APB$ 为直角时,点 $P$ 与点 $C$ 重合,$BP=BC=8\ cm$,即 $t=4$;
②当 $\angle BAP$ 为直角时,$BP=2t\ cm$,$CP=(2t-8)\ cm$,$AC=6\ cm$,
在 $Rt\triangle ACP$ 中,$AP^{2}=6^{2}+(2t-8)^{2}$,
在 $Rt\triangle BAP$ 中,$AB^{2}+AP^{2}=BP^{2}$,即 $10^{2}+[6^{2}+(2t-8)^{2}]=(2t)^{2}$,
解得 $t=\frac{25}{4}$。
综上,当 $\triangle ABP$ 为直角三角形时,$t$ 的值为 4 或 $\frac{25}{4}$。
(3) ①当 $AB=BP$ 时,易得 $t=5$;
②当 $AB=AP$ 时,$BP=2BC=16\ cm$,易得 $t=8$;
③当 $BP=AP$ 时,$AP=BP=2t\ cm$,$CP=|2t-8|\ cm$,$AC=6\ cm$。
在 $Rt\triangle ACP$ 中,$AP^{2}=AC^{2}+CP^{2}$,即 $(2t)^{2}=6^{2}+(2t-8)^{2}$,解得 $t=\frac{25}{8}$。
综上,当 $\triangle ABP$ 为等腰三角形时,$t$ 的值为 5 或 8 或 $\frac{25}{8}$。
查看更多完整答案,请扫码查看


