《2025年南通小题课时作业本八年级数学上册苏科版》

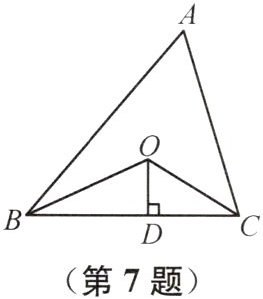
7 (2025盐城月考)如图,△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=4,则△ABC的面积为（C）
A. 84 B. 63 C. 42 D. 21

答案： C

8 (2025盐城月考)如图,AB//CD,PB和PC分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,若AD=8cm,BC=10cm,则四边形ABCD的面积是40$cm^{2}$.

答案： 40

9 (教材P39练习2变式)如图,在△ABC中,∠ABC=48°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠EBF=24°.

答案： $24^{\circ}$

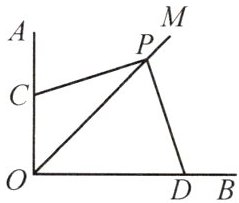
10 如图,∠AOB=90°,OM平分∠AOB,将直角三角板的顶点P在射线OM上移动,两直角边分别与OA,OB相交于点C,D,问PC与PD相等吗?试说明理由.
!

答案：
解：$PC$ 与 $PD$ 相等。理由如下：
如图，过点 $P$ 作 $PE\perp OA$ 于点 $E$，$PF\perp OB$ 于点 $F$。
因为 $OM$ 平分 $\angle AOB$，点 $P$ 在 $OM$ 上，所以 $PE = PF$。
又因为 $\angle AOB = 90^{\circ}$，$\angle PEO=\angle PFO = 90^{\circ}$，
所以 $\angle EPF = 90^{\circ}$，
所以 $\angle EPC+\angle CPF = 90^{\circ}$。
又因为 $\angle CPD = 90^{\circ}$，所以 $\angle CPF+\angle FPD = 90^{\circ}$，
所以 $\angle EPC=\angle FPD = 90^{\circ}-\angle CPF$。
在 $\triangle PCE$ 与 $\triangle PDF$ 中，$\begin{cases}\angle PEC=\angle PFD,\\PE = PF,\\\angle EPC=\angle FPD,\end{cases}$
所以 $\triangle PCE\cong\triangle PDF(ASA)$，所以 $PC = PD$。

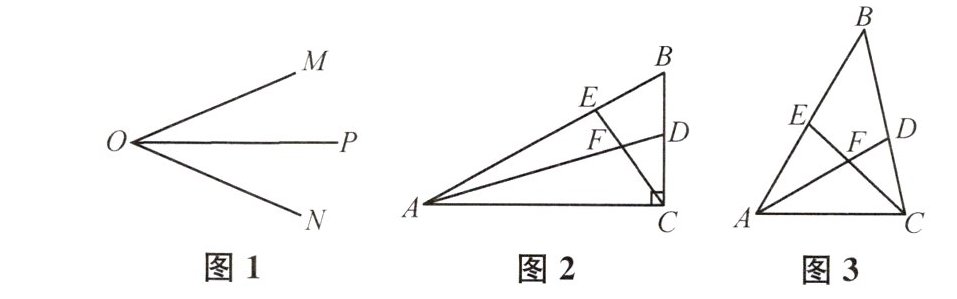
11 新考法 如图1,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形,并将添加的全等条件标注在图上.
请你参考这个作全等三角形的方法,解答下列问题:
(1) 如图2,在△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F,求∠EFA的度数;
(2) 在(1)的条件下,请判断FE与FD之间的数量关系,并说明理由;
(3) 如图3,在△ABC中,如果∠ACB不是直角,且(1)中的其他条件不变,试问在(2)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

答案：
解：全等三角形作法如图1所示，$\triangle BOD\cong\triangle COD$。
(1) 如图2，因为 $\angle ACB = 90^{\circ}$，$\angle B = 60^{\circ}$，
所以 $\angle BAC = 30^{\circ}$。
因为 $AD$，$CE$ 分别是 $\angle BAC$ 和 $\angle BCA$ 的平分线，
所以 $\angle DAC=\frac{1}{2}\angle BAC = 15^{\circ}$，$\angle ECA=\frac{1}{2}\angle ACB = 45^{\circ}$，
所以 $\angle EFA=\angle DAC+\angle ECA = 15^{\circ}+45^{\circ}=60^{\circ}$。
(2) $FE = FD$，理由如下：
如图2，在 $AC$ 上截取 $AG = AE$，连接 $FG$。
因为 $AD$ 是 $\angle BAC$ 的平分线，
所以 $\angle EAF=\angle GAF$。
在 $\triangle EAF$ 和 $\triangle GAF$ 中，$\begin{cases}AE = AG,\\\angle EAF=\angle GAF,\\AF = AF,\end{cases}$
所以 $\triangle EAF\cong\triangle GAF(SAS)$，
所以 $FE = FG$，$\angle EFA=\angle GFA = 60^{\circ}$，
所以 $\angle GFC = 180^{\circ}-60^{\circ}-60^{\circ}=60^{\circ}$，
所以 $\angle DFC=\angle GFC$。
在 $\triangle FDC$ 和 $\triangle FGC$ 中，$\begin{cases}\angle DFC=\angle GFC,\\FC = FC,\\\angle FCG=\angle FCD,\end{cases}$
所以 $\triangle FDC\cong\triangle FGC(ASA)$，
所以 $FD = FG$，所以 $FE = FD$。
(3) $FE = FD$ 仍然成立，理由如下：
如图3，同
(2)可得 $\triangle EAF\cong\triangle HAF$，
所以 $FE = FH$，$\angle EFA=\angle HFA$。
又由
(1)知，$\angle FAC=\frac{1}{2}\angle BAC$，$\angle FCA=\frac{1}{2}\angle ACB$，
所以 $\angle FAC+\angle FCA=\frac{1}{2}(\angle BAC+\angle ACB)=\frac{1}{2}(180^{\circ}-\angle B)=60^{\circ}$，
所以 $\angle AFC = 180^{\circ}-(\angle FAC+\angle FCA)=120^{\circ}$，
所以 $\angle EFA=\angle HFA = 180^{\circ}-120^{\circ}=60^{\circ}$。
同
(2)可得 $\triangle FDC\cong\triangle FHC$，
所以 $FD = FH$，所以 $FE = FD$。