《2025年南通小题课时作业本八年级数学上册苏科版》

9 (易错题)下列所述不属于函数关系的是（D）
A. 长方形的面积一定，它的长和宽的关系
B. $x + 2$与x的关系
C. 匀速运动的火车，时间与路程的关系
D. 某人的身高和体重的关系

答案： D

10 夏季高山上温度从山脚起每升高100m降低$0.7^{\circ}C$。已知山脚下温度是$23^{\circ}C$，则温度$y(^{\circ}C)$与上升高度x(m)之间的关系式为$ y = 23 - 0.007x $。

答案： $ y = 23 - 0.007x $

11 若函数$y = (k - 1)x(k ≠ 1)$，当自变量取值增加2的时候，函数值减少3，则k的值是$ - \frac{1}{2} $。

答案： $ - \frac{1}{2} $

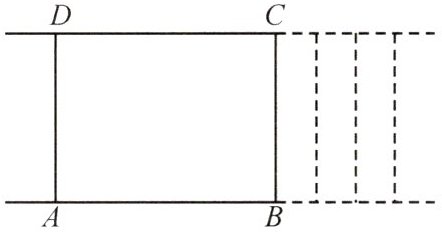
12 如图，长方形ABCD的四个顶点在互相平行的两条直线上，$AD = 20cm$，当点B，C在平行线上同方向匀速运动时，长方形的面积发生了变化。
(1)在这个变化过程中，自变量是什么?
(2)如果长方形的长AB为x(cm)，那么请用含x的式子表示长方形ABCD的面积$y(cm^2)$；
(3)当长方形的长AB从25cm变到40cm时，长方形的面积怎么变化?
!

答案： 解：
(1) 在这个变化过程中，自变量为 $ AB(CD) $ 的长。
(2) $ y = 20x $。
(3) 当 $ AB = 25 \text{ cm} $ 时，$ y = 20x = 20 × 25 = 500(\text{cm}^2) $，
当 $ AB = 40 \text{ cm} $ 时，$ y = 20x = 20 × 40 = 800(\text{cm}^2) $，
所以当长 $ AB $ 从 25 cm 变到 40 cm 时，长方形的面积从 $ 500 \text{ cm}^2 $ 变到 $ 800 \text{ cm}^2 $。

(1)在这个变化过程中，自变量是v；
(2)当刹车时车速为60km/h时，刹车距离是15m；
(3)根据上表反映的规律写出该种型号汽车s与v之间的关系式为s = 0.25v(0 ≤ v ≤ 140)；
(4)该型号汽车在高速公路上发生了一次交通事故，现场测得刹车距离为32m，推测刹车时车速是多少? 并说明事故发生时，汽车是超速行驶还是正常行驶? (相关法规规定：高速公路上行驶的小型载客汽车最高车速不得超过120km/h)
解：当s = 32时，32 = 0.25v，解得v = 128，所以推测刹车时车速是128 km/h。因为120＜128，所以事故发生时，汽车是超速行驶。

答案： 解：
(1) $ v $
(2) 15
(3) $ s = 0.25v(0 \leq v \leq 140) $
(4) 当 $ s = 32 $ 时，$ 32 = 0.25v $，解得 $ v = 128 $，
所以推测刹车时车速是 $ 128 \text{ km/h} $。
因为 $ 120 ＜ 128 $，
所以事故发生时，汽车是超速行驶。