《2025年南通小题课时作业本八年级数学上册苏科版》

7 (2025盐城大丰期末)如图,动点P在平面直角坐标系中按箭头所示方向运动,第1次从原点运动到点$(1,1)$,第2次接着运动到点$(2,0)$,第3次接着运动到点$(3,2),... $,按这样的运动规律,经过第2025次运动后,动点P的坐标是____$(2025,1)$.

答案： $(2025,1)$

在平面直角坐标系中,$△AOB$为等边三角形,点A的坐标为$(1,0)$.把$△AOB$按如图所示的方式放置,并将$△AOB$进行变换:第一次变换将$△AOB$绕着原点O顺时针旋转$60^{\circ }$,同时边长扩大为$△AOB$边长的2倍,得到$△A_{1}OB_{1}$;第二次变换将$△A_{1}OB_{1}$绕着原点O顺时针旋转$60^{\circ }$,同时边长扩大为$△A_{1}OB_{1}$边长的2倍,得到$△A_{2}OB_{2}$,…,依次类推,点$A_{2025}$的坐标为$(-2^{2025},0)$.

答案： $(-2^{2025},0)$

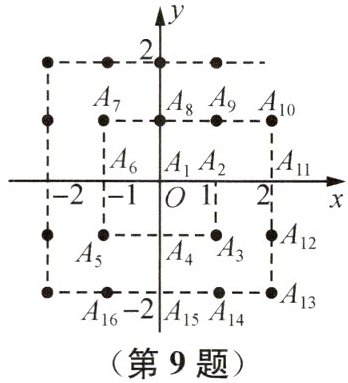
9 (2025盐城盐都月考)数学家高斯被数学界誉为“数学王子”，据传,他在计算$1+2+3+$$4+... +100$时,用到了一种方法,将首尾两个数相加,进而得到$1+2+3+4+... +100=$$\frac {100×(1+100)}{2}$.人们借助于这样的方法,得到$1+2+3+4+... +n=\frac {n(1+n)}{2}$(n是正整数).有下列问题:如图,在平面直角坐标系中的一系列格点$A_{i}(x_{i},y_{i})$,其中$i=1,2,3,...,n,...$,且$x_{i},$$y_{i}$是整数.记$a_{n}=x_{n}+y_{n}$,如$A_{1}(0,0)$,即$a_{1}=0,A_{2}(1,0)$,即$a_{2}=1,A_{3}(1,-1)$,即$a_{3}=0,... ,$以此类推，$a_{2025}=$44.
!

答案： 44

10 (2025无锡锡山月考)如图,在平面直角坐标系中,直线l与x轴交于点$B_{1}$,与y轴交于点D,且$OB_{1}=1,∠ODB_{1}=60^{\circ }$,以$OB_{1}$为边长作等边三角形$A_{1}OB_{1}$,过点$A_{1}$作$A_{1}B_{2}$平行于x轴,交直线l于点$B_{2}$,以$A_{1}B_{2}$为边长作等边三角形$A_{2}A_{1}B_{2}$,过点$A_{2}$作$A_{2}B_{3}$平行于x轴,交直线l于点$B_{3}$,以$A_{2}B_{3}$为边长作等边三角形$A_{3}A_{2}B_{3}$,…,依次进行下去,则点$A_{2022}$的横坐标是$\frac{2^{2022}-1}{2}$.

答案： $\frac{2^{2022}-1}{2}$