第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
10 (2025镇江句容期末)观察表格中的数据:
| x | 32 | 33 | 34 | 35 | 36 | 37 | 38 |
| --- | --- | --- | --- | --- | --- | --- | --- |
| $x^{2}$ | 1 024 | 1 089 | 1 156 | 1 225 | 1 296 | 1 369 | 1 444 |
由表格中的数据可知$\sqrt{12.69}$ (
A. 在3.4~3.5之间
B. 在3.5~3.6之间
C. 在35~36之间
D. 在0.35~0.36之间
| x | 32 | 33 | 34 | 35 | 36 | 37 | 38 |
| --- | --- | --- | --- | --- | --- | --- | --- |
| $x^{2}$ | 1 024 | 1 089 | 1 156 | 1 225 | 1 296 | 1 369 | 1 444 |
由表格中的数据可知$\sqrt{12.69}$ (
B
)A. 在3.4~3.5之间
B. 在3.5~3.6之间
C. 在35~36之间
D. 在0.35~0.36之间
答案:
B
11 (2025南通如皋月考)若m=$\sqrt{38}-4$,则估计m的值所在的范围是 (
A. 1<m<2
B. 2<m<3
C. 3<m<4
D. 4<m<5
B
)A. 1<m<2
B. 2<m<3
C. 3<m<4
D. 4<m<5
答案:
B
12 (2025苏州模拟)已知2a+5的平方根是±3,3a+b-9的立方根是1,c是$\sqrt{3}$的整数部分,则a-b+c的值为
-1
.
答案:
-1
13 (2024南京秦淮期末)因为$\sqrt[3]{1}<\sqrt[3]{3}<\sqrt[3]{8}$,即1<$\sqrt[3]{3}$<2,所以$\sqrt[3]{3}$的整数部分为1,小数部分为$\sqrt[3]{3}-1$,类比以上推理,$\sqrt[3]{30}$的小数部分为
$\sqrt[3]{30} - 3$
.
答案:
$\sqrt[3]{30} - 3$
14 (2024南通期中)
(1)下面是小李探索$\sqrt{2}$的近似值的过程,请补充完整:
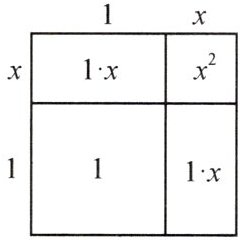
我们知道面积是2的正方形的边长是$\sqrt{2}$,且$\sqrt{2}$>1,设$\sqrt{2}$=1+x,可画出示意图.
由面积公式,可得$x^{2}+2x+1=2$,
略去$x^{2}$,得方程2x+1=2,
解得x=0.5,即$\sqrt{2}$≈______.
上述过程中,主要运用的数学思想是______.
(2)容易知道1<$\sqrt{3}$<2,设$\sqrt{3}$=2-x,请类比(1)中的方法求$\sqrt{3}$的近似值.(要求:画出示意图,标明数据,并写出求解过程)
!
(1)下面是小李探索$\sqrt{2}$的近似值的过程,请补充完整:
我们知道面积是2的正方形的边长是$\sqrt{2}$,且$\sqrt{2}$>1,设$\sqrt{2}$=1+x,可画出示意图.
由面积公式,可得$x^{2}+2x+1=2$,
略去$x^{2}$,得方程2x+1=2,
解得x=0.5,即$\sqrt{2}$≈______.
上述过程中,主要运用的数学思想是______.
(2)容易知道1<$\sqrt{3}$<2,设$\sqrt{3}$=2-x,请类比(1)中的方法求$\sqrt{3}$的近似值.(要求:画出示意图,标明数据,并写出求解过程)
!

答案:
(1) 1.5 数形结合思想
(2) 解: 如图, 设 $\sqrt{3} = 2 - x$, 则 $(2 - x)^2 = 3$,
根据图中面积可得 $2^2 - 2x(2 - x) - x^2 = 3$,
所以 $4 - 4x + x^2 = 3$,
略去 $x^2$, 得方程 $4 - 4x = 3$, 所以 $x = 0.25$,
所以 $\sqrt{3} \approx 2 - 0.25 = 1.75$.

(1) 1.5 数形结合思想
(2) 解: 如图, 设 $\sqrt{3} = 2 - x$, 则 $(2 - x)^2 = 3$,
根据图中面积可得 $2^2 - 2x(2 - x) - x^2 = 3$,
所以 $4 - 4x + x^2 = 3$,
略去 $x^2$, 得方程 $4 - 4x = 3$, 所以 $x = 0.25$,
所以 $\sqrt{3} \approx 2 - 0.25 = 1.75$.

(1)当x=16时,y的值为
(2)是否存在输入有意义的x值后,却始终输不出y值?如果存在,写出所有满足要求的x值;如果不存在,请说明理由;
(3)如果输入x值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的x值可能是什么情况?
(4)当输出的y值是$\sqrt{3}$时,判断输入的x值是否唯一?如果不唯一,请写出其中的三个.
$\sqrt{2}$
;(2)是否存在输入有意义的x值后,却始终输不出y值?如果存在,写出所有满足要求的x值;如果不存在,请说明理由;
当$x = 0$或$x = 1$时,始终输不出$y$值.因为0,1的算术平方根分别是0,1,一定是有理数.
(3)如果输入x值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的x值可能是什么情况?
当$x < 0$时,导致开平方运算无法进行.
(4)当输出的y值是$\sqrt{3}$时,判断输入的x值是否唯一?如果不唯一,请写出其中的三个.
$x$的值不唯一.$x = 3$或$x = 9$或$x = 81$等.
答案:
解:
(1) $\sqrt{2}$
(2) 当 $x = 0$ 或 $x = 1$ 时, 始终输不出 $y$ 值.
因为 0,1 的算术平方根分别是 0,1, 一定是有理数.
(3) 当 $x < 0$ 时, 导致开平方运算无法进行.
(4) $x$ 的值不唯一. $x = 3$ 或 $x = 9$ 或 $x = 81$ 等.
(1) $\sqrt{2}$
(2) 当 $x = 0$ 或 $x = 1$ 时, 始终输不出 $y$ 值.
因为 0,1 的算术平方根分别是 0,1, 一定是有理数.
(3) 当 $x < 0$ 时, 导致开平方运算无法进行.
(4) $x$ 的值不唯一. $x = 3$ 或 $x = 9$ 或 $x = 81$ 等.
查看更多完整答案,请扫码查看


