第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1(2025泰州兴化期末)如图,小明书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是 (
A. SSS
B. SAS
C. SSA
D. ASA
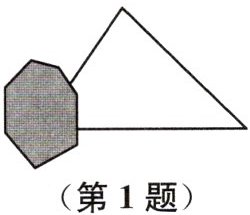
D
)A. SSS
B. SAS
C. SSA
D. ASA

答案:
D
2如图,AB=DB,BC=BE,若要证△ABE≌△DBC,则可增加的条件是 (
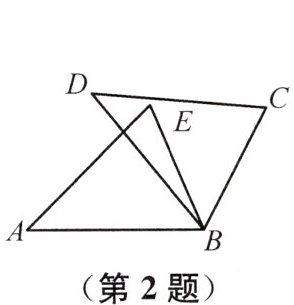
A. ∠ABE=∠DBE
B. ∠A=∠D
C. ∠E=∠C
D. ∠ABD=∠EBC
D
)
A. ∠ABE=∠DBE
B. ∠A=∠D
C. ∠E=∠C
D. ∠ABD=∠EBC
答案:
D
3(2024南京江宁月考)如图,已知∠CAE=∠BAD,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有 (

A. 1个
B. 2个
C. 3个
D. 4个
C
)
A. 1个
B. 2个
C. 3个
D. 4个
答案:
C
4新情境如图,把一长一短两根细木棍的一端用绳子绑在一起,使长木棍的另一端与射线BC的端点B重合,固定住长木棍,把短木棍摆动,端点落在射线BC上的C,D两点位置时,形成的△OBD和△OBC中有OB=OB,OC=OD,∠OBD=∠DBO,则△OBD与△OCB______(填“全等”或“不全等”),这说明______.
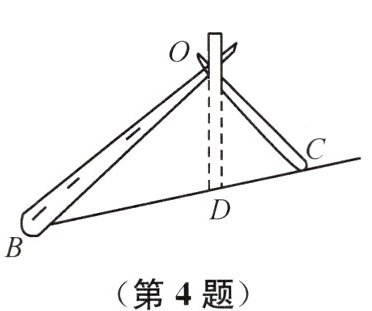

不全等
两边及一边对角对应相等的两个三角形不一定全等
答案:
不全等 两边及一边对角对应相等的两个三角形不一定全等
5(2025泰州姜堰月考)如图,AB⊥CD,且AB=CD,E,F是AD上两点,CF⊥AD,BE⊥AD.若CF=8,BE=6,AD=10,则EF的长为
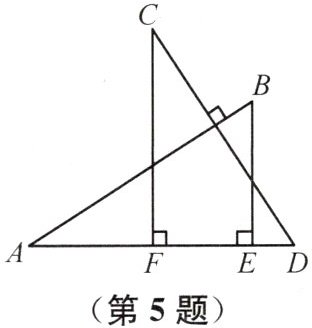
4
.
答案:
4
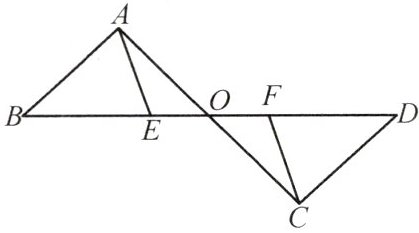
6(2025苏州工业园区期中)如图,点E,F在线段BD上,且AB=CD,BF=DE,AE=CF,AC与BD相交于点O,求证:OA=OC.
!
!

答案:
证明:因为 $ BF = DE $,
所以 $ BF - EF = DE - EF $,即 $ BE = DF $。
又因为 $ AB = CD $,$ AE = CF $,
所以 $ \triangle ABE \cong \triangle CDF(SSS) $,
所以 $ \angle B = \angle D $。
又 $ AB = CD $,$ \angle AOB = \angle COD $,
所以 $ \triangle ABO \cong \triangle CDO(AAS) $,
所以 $ OA = OC $。
所以 $ BF - EF = DE - EF $,即 $ BE = DF $。
又因为 $ AB = CD $,$ AE = CF $,
所以 $ \triangle ABE \cong \triangle CDF(SSS) $,
所以 $ \angle B = \angle D $。
又 $ AB = CD $,$ \angle AOB = \angle COD $,
所以 $ \triangle ABO \cong \triangle CDO(AAS) $,
所以 $ OA = OC $。
7(2024长沙)如图,点C在线段AD上,AB=AD,∠B=∠D,BC=DE.
(1) 求证:△ABC≌△ADE;
(2) 若∠BAC=60°,求∠ACE的度数.
!

(1) 求证:△ABC≌△ADE;
(2) 若∠BAC=60°,求∠ACE的度数.
!

答案:
(1) 证明:在 $ \triangle ABC $ 和 $ \triangle ADE $ 中,$ \left\{ \begin{array} { l } { BC = DE, } \\ { \angle B = \angle D, } \\ { AB = AD, } \end{array} \right. $
所以 $ \triangle ABC \cong \triangle ADE(SAS) $。
(2) 解:由
(1),得 $ \triangle ABC \cong \triangle ADE $,
所以 $ AC = AE $,$ \angle BAC = \angle DAE = 60 ^ { \circ } $,
所以 $ \angle AEC = \angle ACE $。
因为 $ \angle AEC + \angle ACE = 2 \angle ACE = 180 ^ { \circ } - \angle DAE = 120 ^ { \circ } $,
所以 $ \angle ACE = 60 ^ { \circ } $。
故 $ \angle ACE $ 的度数是 $ 60 ^ { \circ } $。
(1) 证明:在 $ \triangle ABC $ 和 $ \triangle ADE $ 中,$ \left\{ \begin{array} { l } { BC = DE, } \\ { \angle B = \angle D, } \\ { AB = AD, } \end{array} \right. $
所以 $ \triangle ABC \cong \triangle ADE(SAS) $。
(2) 解:由
(1),得 $ \triangle ABC \cong \triangle ADE $,
所以 $ AC = AE $,$ \angle BAC = \angle DAE = 60 ^ { \circ } $,
所以 $ \angle AEC = \angle ACE $。
因为 $ \angle AEC + \angle ACE = 2 \angle ACE = 180 ^ { \circ } - \angle DAE = 120 ^ { \circ } $,
所以 $ \angle ACE = 60 ^ { \circ } $。
故 $ \angle ACE $ 的度数是 $ 60 ^ { \circ } $。
查看更多完整答案,请扫码查看


