《2025年全优课堂考点集训与满分备考九年级数学下册冀教版》

18. 较难题 某学校游戏节活动中，设计了一个有奖转盘游戏，如图，A转盘被分成三个面积相等的扇形，B转盘被分成四个面积相等的扇形，每一个扇形都标有相应的数字，先转动A转盘，记下指针所指区域内的数字，再转动B转盘，记下指针所指区域内的数字（当指针在边界线上时，重新转动一次，直到指针指向一个区域内为止），然后，将两次记录的数据相乘.
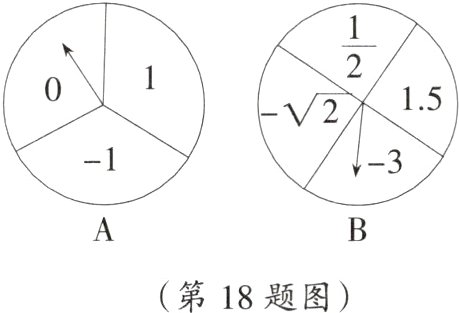
（1）请利用列表格的方法，求出乘积结果为负数的概率；
（2）如果乘积是无理数时获得一等奖，那么获得一等奖的概率是多少？
　　　　　　　　

答案：
解:
(1)列表如下:

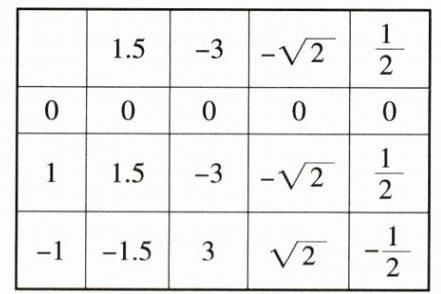
所有等可能的情况有 12 种,乘积结果为负数的情况有 4 种,则 $P($乘积结果为负数$)=\frac{4}{12}=\frac{1}{3}$;
(2)由
(1)中表格知乘积是无理数的情况有 2 种,则 $P($乘积为无理数$)=\frac{2}{12}=\frac{1}{6}$,
∴ 获得一等奖的概率是 $\frac{1}{6}$.

19. 如图，管中放置着三根同样的绳子AA₁，BB₁，CC₁.
（1）小明从这三根绳子中随机选一根，恰好选中绳子AA₁的概率是多少？
（2）小明先从左端A，B，C三个绳头中随机选两个打一个结，再从右端A₁，B₁，C₁三个绳头中随机选两个打一个结，求这三根绳子能连接成一根长绳的概率.
　　　　　　

答案：
解:
(1)小明可选择的情况有 3 种,每种情况发生的可能性相等,则小明恰好选中绳子 $AA_1$ 的概率 $P = \frac{1}{3}$;
(2)根据题意可知:分别在两端随机任选两个绳头打结,总共有 9 种情况,列表如下:

其中左右打结是相同字母(不考虑下标)的情况,不可能连接成一根长绳,所以能连接成一根长绳的情况有 6 种:①左端连 $AB$,右端连 $A_1C_1$ 或 $B_1C_1$;②左端连 $BC$,右端连 $A_1B_1$ 或 $A_1C_1$;③左端连 $AC$,右端连 $A_1B_1$ 或 $B_1C_1$.故这三根绳子能连接成一条长绳的情况有 6 种, $P=\frac{6}{9}=\frac{2}{3}$.

20. 中考新情境 推理能力 在一个不透明的口袋里装有分别标注2，4，6的3个小球（小球除数字不同外，其余都相同），另有3张背面完全一样，正面分别写有数字6，7，8的卡片.现从口袋中任意摸出一个小球，再从这3张背面朝上的卡片中任意摸出一张卡片.
（1）请你用列表的方法，表示出所有可能出现的结果；
（2）小红和小莉做游戏，制定了如下两个游戏规则：
规则1：若两次摸出的数字，至少有一次是“6”，小红赢；否则，小莉赢.
规则2：若摸出的卡片上的数字是球上数字的整数倍时，小红赢；否则，小莉赢.
小红要想在游戏中获胜，她会选择哪一种规则，并说明理由.

答案：
解:
(1)列表如下:

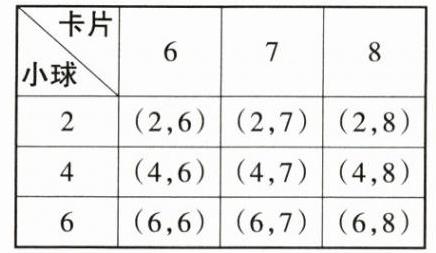
(2)规则 1.理由:从表可知,共有 9 种等可能的结果,至少有一次是“6”的结果有 5 种,没有一次是“6”的结果有 4 种,
∴ 小红赢的概率 $P($至少有一次是“6”$)=\frac{5}{9}$,小莉赢的概率是 $\frac{4}{9}$,
$\because\frac{5}{9}＞\frac{4}{9}$,
∴ 对于规则 1,小红获胜的概率大;卡片上的数字是球上数字的整数倍的有: $(2,6)$, $(2,8)$, $(4,8)$, $(6,6)$,共 4 种结果,卡片上的数字不是球上数字的整数倍的有: $(2,7)$, $(4,6)$, $(4,7)$, $(6,7)$, $(6,8)$,共有 5 种结果,
∴ 小红赢的概率是 $P($卡片上的数字是球上数字的整数倍$)=\frac{4}{9}$,小莉赢的概率是 $\frac{5}{9}$, $\because\frac{5}{9}＞\frac{4}{9}$,
∴ 对于规则 2,小莉获胜的概率大,
∴ 小红要想在游戏中获胜,她应该选择规则 1.