2025年全优课堂考点集训与满分备考九年级数学下册冀教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全优课堂考点集训与满分备考九年级数学下册冀教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第88页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
1. 习题高仿教材P83,AT3改编 从1,2,3,4,5,6六个数中任取2个数,则取出的两个数不是连续自然数的概率是 ( )
A. $\frac{3}{5}$
B. $\frac{2}{5}$
C. $\frac{1}{3}$
D. $\frac{2}{3}$
A. $\frac{3}{5}$
B. $\frac{2}{5}$
C. $\frac{1}{3}$
D. $\frac{2}{3}$
答案:
D 提示:列表如下:
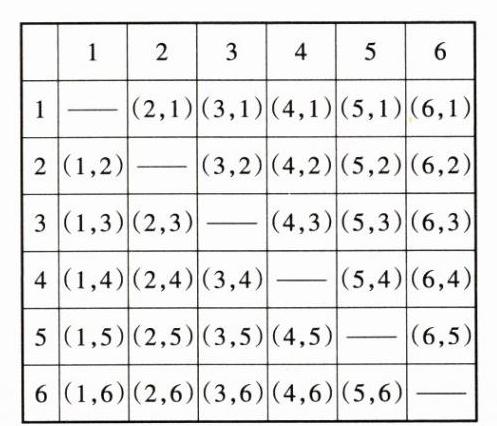
由表可知共有 30 种等可能结果,其中取出的两个数不是连续自然数的有 20 种结果,所以取出的两个数不是连续自然数的概率为 $\frac{20}{30}=\frac{2}{3}$.
D 提示:列表如下:

由表可知共有 30 种等可能结果,其中取出的两个数不是连续自然数的有 20 种结果,所以取出的两个数不是连续自然数的概率为 $\frac{20}{30}=\frac{2}{3}$.
2. 习题变式教材P80,AT1改编 书架上放着三本古典名著和两本外国小说,小明从中随机抽取两本,两本都是古典名著的概率是 ( )
A. $\frac{4}{25}$
B. $\frac{9}{25}$
C. $\frac{3}{10}$
D. $\frac{1}{10}$
A. $\frac{4}{25}$
B. $\frac{9}{25}$
C. $\frac{3}{10}$
D. $\frac{1}{10}$
答案:
C 提示:用 $A_1$, $A_2$, $A_3$ 表示古典名著, $B_1$, $B_2$ 表示外国小说.用列表法列出所有可能出现的情况如下:
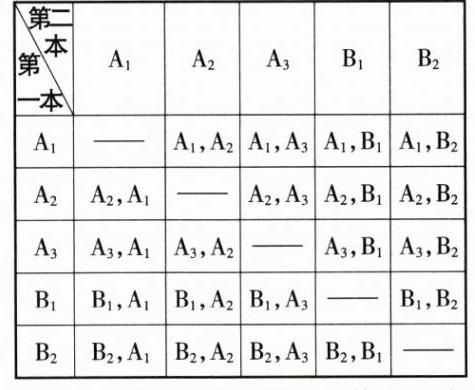
共有 20 种等可能的情况,其中两本都是古典名著的有 6 种,所以 $P($两本都是古典名著$)=\frac{6}{20}=\frac{3}{10}$.
C 提示:用 $A_1$, $A_2$, $A_3$ 表示古典名著, $B_1$, $B_2$ 表示外国小说.用列表法列出所有可能出现的情况如下:

共有 20 种等可能的情况,其中两本都是古典名著的有 6 种,所以 $P($两本都是古典名著$)=\frac{6}{20}=\frac{3}{10}$.
3. 习题高仿教材P80,BT2改编 一个不透明的口袋中装有仅颜色不同的2个红球和2个白球,两个人依次从袋中随机摸出一个小球不放回,则第一个人摸到红球且第二个人摸到白球的概率是 __________.
答案:
$\frac{1}{3}$
4. 习题变式教材P80,AT2改编 如图,两个圆盘中,指针落在每一个数上机会都相等,那么当两个指针所指数的乘积不为6的整数倍时,它的概率为 __________.
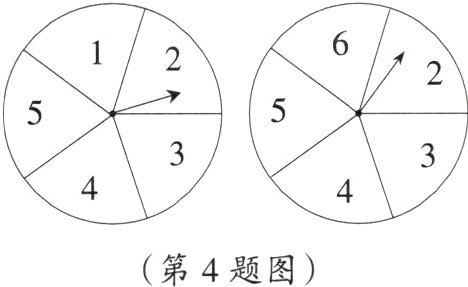

答案:
$\frac{16}{25}$
5. 习题变式教材P80,AT2改编 在一个不透明的口袋里装有标号分别为1,2,3,4,5的五个球,除数字不同外,没有任何区别,摸球前先搅拌均匀,每次摸一个球.
(1)给出下列说法:
①摸一次,摸出1号球和摸出5号球的概率相同;
②有放回地连续摸10次,则一定摸出2号球两次;
③有放回地连续摸4次,则摸出四个球标号数字之和可能是20.
其中正确的序号是 ________;
(2)若从袋中不放回地摸两次,求两球标号数字是一奇一偶的概率.
(1)给出下列说法:
①摸一次,摸出1号球和摸出5号球的概率相同;
②有放回地连续摸10次,则一定摸出2号球两次;
③有放回地连续摸4次,则摸出四个球标号数字之和可能是20.
其中正确的序号是 ________;
(2)若从袋中不放回地摸两次,求两球标号数字是一奇一偶的概率.
答案:
解:
(1)①③ 提示:①摸一次,摸出 1 号球与摸出 5 号球的概率相同,均为 $\frac{1}{5}$,故正确;②有放回地连续摸 10 次,不一定摸出 2 号球,故错误;③有放回地连续摸 4 次,若 4 次均摸出标号为 5 的球, $5 + 5+5 + 5 = 20$,则摸出四个球标号数字之和可能是 20;
(2)列表如下:

所有等可能的情况有 20 种,其中摸出的两球标号数字是一奇一偶的情况有 12 种,
则 $P($一奇一偶$)=\frac{12}{20}=\frac{3}{5}$.
解:
(1)①③ 提示:①摸一次,摸出 1 号球与摸出 5 号球的概率相同,均为 $\frac{1}{5}$,故正确;②有放回地连续摸 10 次,不一定摸出 2 号球,故错误;③有放回地连续摸 4 次,若 4 次均摸出标号为 5 的球, $5 + 5+5 + 5 = 20$,则摸出四个球标号数字之和可能是 20;
(2)列表如下:

所有等可能的情况有 20 种,其中摸出的两球标号数字是一奇一偶的情况有 12 种,
则 $P($一奇一偶$)=\frac{12}{20}=\frac{3}{5}$.
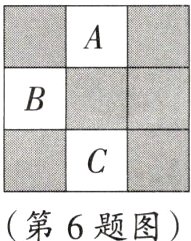
6. 在如图所示的方格地面上,标有编号分别为A,B,C的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同.
(1)一只自由飞行的鸟,将随意地落在图中的方格地面上,小鸟落在草坪上的概率是_____;
(2)现从3个小方格空地中任意选取2个种植草坪,则刚好选取A和B的2个小方格空地种植草坪的概率是 ________.
(1)一只自由飞行的鸟,将随意地落在图中的方格地面上,小鸟落在草坪上的概率是_____;
(2)现从3个小方格空地中任意选取2个种植草坪,则刚好选取A和B的2个小方格空地种植草坪的概率是 ________.

答案:
(1) $\frac{2}{3}$
(2) $\frac{1}{3}$
提示:
(1) $P($小鸟落在草坪上$)=\frac{6}{9}=\frac{2}{3}$;
(2)列表格写出所有情况的可能的结果如下:
| | $A$ | $B$ | $C$ |
| --- | --- | --- | --- |
| $A$ | —— | $(A,B)$ | $(A,C)$ |
| $B$ | $(B,A)$ | —— | $(B,C)$ |
| $C$ | $(C,A)$ | $(C,B)$ | —— |
由表格可知,共有 6 种等可能结果,编号为 $A$, $B$ 的 2 个小方格空地种植草坪的结果有 2 种,所以 $P($编号为 $A$, $B$ 的 2 个小方格空地种植草坪$)=\frac{2}{6}=\frac{1}{3}$.
(1) $\frac{2}{3}$
(2) $\frac{1}{3}$
提示:
(1) $P($小鸟落在草坪上$)=\frac{6}{9}=\frac{2}{3}$;
(2)列表格写出所有情况的可能的结果如下:
| | $A$ | $B$ | $C$ |
| --- | --- | --- | --- |
| $A$ | —— | $(A,B)$ | $(A,C)$ |
| $B$ | $(B,A)$ | —— | $(B,C)$ |
| $C$ | $(C,A)$ | $(C,B)$ | —— |
由表格可知,共有 6 种等可能结果,编号为 $A$, $B$ 的 2 个小方格空地种植草坪的结果有 2 种,所以 $P($编号为 $A$, $B$ 的 2 个小方格空地种植草坪$)=\frac{2}{6}=\frac{1}{3}$.
查看更多完整答案,请扫码查看


