2025年全优课堂考点集训与满分备考九年级数学下册冀教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全优课堂考点集训与满分备考九年级数学下册冀教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
4. 易错题 某景点商户抓住商机,向游客推销一种加工好的喂养海鸥的饲料,已知每千克成本为20元,市场调查发现,在一段时间内,该产品每天销售量w(kg)随销售单价x(元/kg)的变化而变化,有这样的关系式:w = -2x + 80。设这种饲料在这段时间内的销售利润为y(元)。
(1)当销售单价定为多少元时,每天的销售利润最大?最大利润是多少?
(2)如果物价部门规定该景区这种饲料的销售单价不得高于28元/kg,该商户每天能否获得比150元更大的利润?如果能,请求出最大利润,如果不能,请说明理由。
(1)当销售单价定为多少元时,每天的销售利润最大?最大利润是多少?
(2)如果物价部门规定该景区这种饲料的销售单价不得高于28元/kg,该商户每天能否获得比150元更大的利润?如果能,请求出最大利润,如果不能,请说明理由。
答案:
解:
(1)由题意得y = (x - 20)( - 2x + 80)= - 2x² + 80x + 40x - 1600 = - 2x² + 120x - 1600 = - 2(x - 30)² + 200,
∵a = - 2 < 0,
∴抛物线开口向下,
∵x ≥ 20,y ≥ 0,
∴20 ≤ x ≤ 40,
∴当x = 30时,y最大 = 200,即销售单价定为30元/kg时,每天的销售利润最大,最大利润是200元;
(2)
∵y = - 2(x - 30)² + 200,
∴当x < 30时y随x增大而增大,
∵x ≤ 28,
∴当x = 28时,y能取得最大值为192,即商户每天能获得比150元更大的利润,最大利润是192元.
(1)由题意得y = (x - 20)( - 2x + 80)= - 2x² + 80x + 40x - 1600 = - 2x² + 120x - 1600 = - 2(x - 30)² + 200,
∵a = - 2 < 0,
∴抛物线开口向下,
∵x ≥ 20,y ≥ 0,
∴20 ≤ x ≤ 40,
∴当x = 30时,y最大 = 200,即销售单价定为30元/kg时,每天的销售利润最大,最大利润是200元;
(2)
∵y = - 2(x - 30)² + 200,
∴当x < 30时y随x增大而增大,
∵x ≤ 28,
∴当x = 28时,y能取得最大值为192,即商户每天能获得比150元更大的利润,最大利润是192元.
5. 模型观念 某企业接到一批粽子生产任务,按要求在19天内完成,约定这批粽子的出厂价为每只4元,为按时完成任务,该企业招收了新工人,设新工人李红第x天生产的粽子数量为y只,y与x满足如下关系:$y=\begin{cases}32x(0\leq x\leq5),\\20x + 60(5\lt x\leq19).\end{cases}$
(1)李红第几天生产的粽子数量为260只?
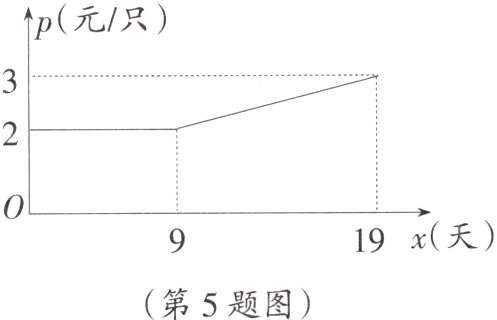
(2)如图,设第x天生产的每只粽子的成本是p元,p与x之间的关系可用图中的函数图像来刻画,若李红第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元。(利润 = 出厂价 - 成本)
(1)李红第几天生产的粽子数量为260只?
(2)如图,设第x天生产的每只粽子的成本是p元,p与x之间的关系可用图中的函数图像来刻画,若李红第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元。(利润 = 出厂价 - 成本)

答案:
解:
(1)设李红第x天生产的粽子数量为260只,
∵32×5 = 160 < 260,
∴5 < x ≤ 19.根据题意得20x + 60 = 260,解得x = 10,即李红第10天生产的粽子数量为260只;
(2)根据图像得当0 ≤ x ≤ 9时,p = 2;当9 < x ≤ 19时,设解析式为p = kx + b,把(9,2),(19,3)代入得$\begin{cases}9k + b = 2 \\19k + b = 3\end{cases}$,解得$\begin{cases}k = \frac{1}{10} \\b = \frac{11}{10}\end{cases}$,
∴p = $\frac{1}{10}$x + $\frac{11}{10}$,①当0 ≤ x ≤ 5时,w = (4 - 2)×32x = 64x,当x = 5时,w最大 = 320元;②当5 < x ≤ 9时,w = (4 - 2)×(20x + 60)= 40x + 120,当x = 9时,w最大 = 480元;③当9 < x ≤ 19时,w = [4 - ($\frac{1}{10}$x + $\frac{11}{10}$)]·(20x + 60)= - 2x² + 52x + 174 = - 2(x - 13)² + 512,当x = 13时,w最大 = 512元.综上所述,第13天的利润最大,最大利润是512元.
(1)设李红第x天生产的粽子数量为260只,
∵32×5 = 160 < 260,
∴5 < x ≤ 19.根据题意得20x + 60 = 260,解得x = 10,即李红第10天生产的粽子数量为260只;
(2)根据图像得当0 ≤ x ≤ 9时,p = 2;当9 < x ≤ 19时,设解析式为p = kx + b,把(9,2),(19,3)代入得$\begin{cases}9k + b = 2 \\19k + b = 3\end{cases}$,解得$\begin{cases}k = \frac{1}{10} \\b = \frac{11}{10}\end{cases}$,
∴p = $\frac{1}{10}$x + $\frac{11}{10}$,①当0 ≤ x ≤ 5时,w = (4 - 2)×32x = 64x,当x = 5时,w最大 = 320元;②当5 < x ≤ 9时,w = (4 - 2)×(20x + 60)= 40x + 120,当x = 9时,w最大 = 480元;③当9 < x ≤ 19时,w = [4 - ($\frac{1}{10}$x + $\frac{11}{10}$)]·(20x + 60)= - 2x² + 52x + 174 = - 2(x - 13)² + 512,当x = 13时,w最大 = 512元.综上所述,第13天的利润最大,最大利润是512元.
6. 某公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为$p=\begin{cases}\frac{1}{4}t + 30(1\leq t\leq24,t为整数),\\-\frac{1}{2}t + 48(25\leq t\leq48,t为整数),\end{cases}$且其日销售量y(kg)与时间t(天)的关系如表:

(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少;
(2)哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每天每销售1kg水果就捐赠n元(n<9)给偏远山区学生。现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围。

(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少;
(2)哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每天每销售1kg水果就捐赠n元(n<9)给偏远山区学生。现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围。
答案:
解:
(1)依题意,设y = kt + b,将(10,100),(20,80)代入y = kt + b,得$\begin{cases}100 = 10k + b \\80 = 20k + b\end{cases}$,解得$\begin{cases}k = - 2 \\b = 120\end{cases}$,
∴日销售量y(kg)与时间t(天)的关系为y = - 2t + 120,当t = 30时,y = - 2×30 + 120 = 60,
∴在第30天的日销售量是60 kg;
(2)设日销售利润为W元,则W = (p - 20)y.当1 ≤ t ≤ 24时,W = ($\frac{1}{4}$t + 30 - 20)(120 - 2t)= - $\frac{1}{2}$t² + 10t + 1200 = - $\frac{1}{2}$(t - 10)² + 1250,当t = 10时,W最大 = 1250.当25 ≤ t ≤ 48时,W = ( - $\frac{1}{2}$t + 48 - 20)·(120 - 2t)= t² - 116t + 3360 = (t - 58)² - 4,由二次函数的图像及性质知:当t = 25时,W最大 = 1085.
∵1250 > 1085,
∴在第10天的销售利润最大,最大利润为1250元;
(3)依题意得,在前24天中,每天扣除捐赠后的日销售利润为W = ($\frac{1}{4}$t + 30 - 20 - n)(120 - 2t)= - $\frac{1}{2}$t² + (2n + 10)t + 1200 - 120n,其图像对称轴为直线t = 2n + 10,要使W随t的增大而增大,由二次函数的图像及性质知:2n + 10 ≥ 24,解得n ≥ 7.又
∵n < 9,
∴7 ≤ n < 9.
(1)依题意,设y = kt + b,将(10,100),(20,80)代入y = kt + b,得$\begin{cases}100 = 10k + b \\80 = 20k + b\end{cases}$,解得$\begin{cases}k = - 2 \\b = 120\end{cases}$,
∴日销售量y(kg)与时间t(天)的关系为y = - 2t + 120,当t = 30时,y = - 2×30 + 120 = 60,
∴在第30天的日销售量是60 kg;
(2)设日销售利润为W元,则W = (p - 20)y.当1 ≤ t ≤ 24时,W = ($\frac{1}{4}$t + 30 - 20)(120 - 2t)= - $\frac{1}{2}$t² + 10t + 1200 = - $\frac{1}{2}$(t - 10)² + 1250,当t = 10时,W最大 = 1250.当25 ≤ t ≤ 48时,W = ( - $\frac{1}{2}$t + 48 - 20)·(120 - 2t)= t² - 116t + 3360 = (t - 58)² - 4,由二次函数的图像及性质知:当t = 25时,W最大 = 1085.
∵1250 > 1085,
∴在第10天的销售利润最大,最大利润为1250元;
(3)依题意得,在前24天中,每天扣除捐赠后的日销售利润为W = ($\frac{1}{4}$t + 30 - 20 - n)(120 - 2t)= - $\frac{1}{2}$t² + (2n + 10)t + 1200 - 120n,其图像对称轴为直线t = 2n + 10,要使W随t的增大而增大,由二次函数的图像及性质知:2n + 10 ≥ 24,解得n ≥ 7.又
∵n < 9,
∴7 ≤ n < 9.
查看更多完整答案,请扫码查看


