《2025年全优课堂考点集训与满分备考九年级数学下册冀教版》

7. 某种正方形合金板材的成本y(元)与它的面积成正比，设边长为x cm.当x=3时，y=18，那么当成本为72元时，边长为 ( )
A. 6 cm
B. 12 cm
C. 24 cm
D. 36 cm

答案： A

8. 在一定条件下，若物体运动的路程s(m)与时间t(s)的关系式为s=5$t^{2}$+2t，则当物体运动的路程是88 m时，该物体运动的时间为 ( )
A. 2 s
B. 4 s
C. 6 s
D. 8 s

答案： B

9. 易错题 一支某品牌钢笔进价8元，按10元1支出售时每天能卖出20支，市场调查发现如果每支每涨价1元，每天就少卖出2支，为了每天获得最大利润，其销售单价应定为 ( )
A. 11元
B. 12元
C. 13元
D. 14元

答案： D

10. 某玩具厂计划生产一种玩具熊猫，每日最高产量为40只，且每日产出的产品全部售出.已知生产x只玩具熊猫的成本为R(元)，每只售价为P(元)，且R，P与x的关系式分别为R=30x+500，P=170 - 2x，若可获得的最大利润为1 950元，则日产量为 ( )
A. 25只
B. 30只
C. 35只
D. 40只

答案： C

11. 一名男生推铅球，铅球行进高度y(单位：m)与水平距离x(单位：m)之间的关系是y=-$\frac{6}{11}$·$x^{2}+\frac{30}{11}x+\frac{3}{2}$，则他将铅球推出的距离是______ m.

答案： 5.5 m

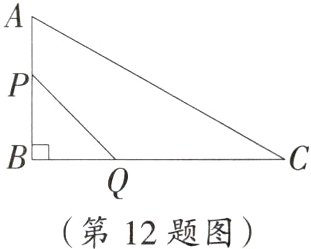
12. 数形结合思想 如图，在△ABC中，∠B=90°，AB=12 mm，BC=24 mm，动点P从点A开始沿边AB向点B以2 mm/s的速度移动(不与点B重合)，动点Q从点B开始沿边BC向点C以4 mm/s的速度移动(不与点C重合).如果点P，Q分别从点A，B同时出发，那么经过______ s，四边形APQC的面积最小.

答案： 3 提示：设点$P$，$Q$同时出发后经过的时间为$t$ s，四边形$APQC$的面积为$S$ $mm^2$，则有$S = S_{\triangle ABC}-S_{\triangle PBQ}=\frac{1}{2}\times12\times24-\frac{1}{2}\times4t\times(12 - 2t)=4t^2 - 24t + 144=4(t - 3)^2 + 108$.
$\because4\gt0$，
$\therefore$当$t = 3$时，$S$取得最小值.

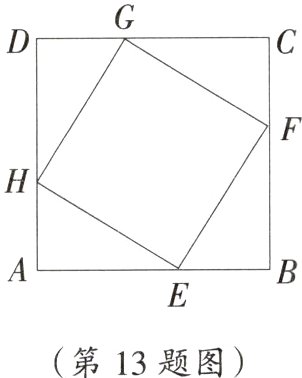
13. 几何直观 如图，点E，F，G，H分别位于边长为a的正方形ABCD的四条边上，四边形EFGH也是正方形，AE=x，正方形EFGH的面积为y.
(1)当a=2，y=3时，求x的值；
(2)当x为何值时，y的值最小?最小值是多少?

答案： 解：
(1)$AE = x$，则$BE = a - x$，
$\because$四边形$EFGH$是正方形，
$\therefore EH = EF$，$\angle HEF = 90^{\circ}$，
$\therefore\angle AEH+\angle BEF = 90^{\circ}$，
$\because\angle AEH+\angle AHE = 90^{\circ}$，$\therefore\angle AHE=\angle BEF$，在$\triangle AHE$和$\triangle BEF$中，
$\begin{cases}\angle A=\angle B = 90^{\circ},\\\angle AHE=\angle BEF,\\EH = FE,\end{cases}$
$\therefore\triangle AHE\cong\triangle BEF(AAS)$，同理可证$\triangle AHE\cong\triangle BEF\cong\triangle CFG\cong\triangle DGH$，
$\therefore AE = BF = CG = DH = x$，$AH = BE = CF = DG = a - x$，$\therefore EF^2 = BE^2 + BF^2=(a - x)^2 + x^2=2x^2 - 2ax + a^2$，
$\therefore$正方形$EFGH$的面积$y = EF^2=2x^2 - 2ax + a^2$，
当$a = 2$，$y = 3$时，$2x^2 - 4x + 4 = 3$，解得$x=\frac{2\pm\sqrt{2}}{2}$；
(2)$\because y = 2x^2 - 2ax + a^2=2(x-\frac{1}{2}a)^2+\frac{1}{2}\cdot a^2$，即当$x=\frac{1}{2}a$（即$E$在$AB$边上的中点）时，正方形$EFGH$的面积最小，最小的面积为$\frac{1}{2}a^2$.

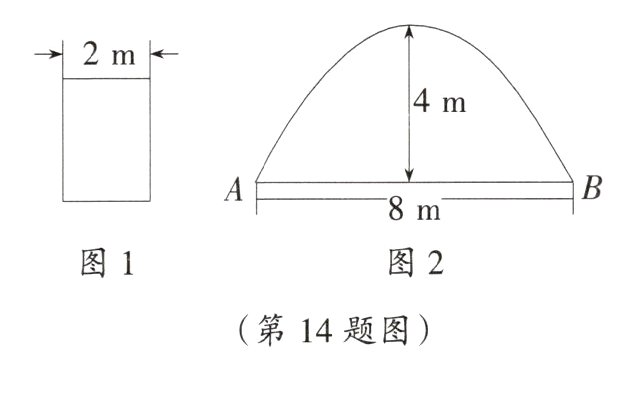
14. 模型观念 有一辆宽为2 m的货车 (如图1)，要通过一条抛物线形隧道(如图2).为确保车辆安全通行，规定货车车顶左右两侧离隧道内壁的垂直高度至少为0.5 m.已知隧道的跨度AB为8 m，拱高为4 m.
(1)若隧道为单车道，货车的高为3.2 m，该货车能否安全通行? 为什么?
(2)若隧道为双车道，且两车道之间有0.4 m的隔离带，通过计算说明该货车能够通行的最大安全限高.

答案： 解：
(1)货车能安全通行.在题图中以$AB$所在直线为$x$轴，$AB$中点为原点，建立平面直角坐标系，设抛物线解析式为$y = ax^2 + 4$，将$(4,0)$代入得$16a + 4 = 0$，解得$a=-\frac{1}{4}$，
$\therefore$抛物线表达式为$y=-\frac{1}{4}x^2 + 4$.由$x = 1$可得，$y = 3.75$.
$\because3.75 - 0.5 = 3.25\gt3.2$，
$\therefore$货车能够安全通行；
(2)由$x=\frac{11}{5}$可得，$y = 2.79$.$\because2.79 - 0.5 = 2.29$，$\therefore$货车能够通行的最大安全限高为2.29 m.

15. 方程思想 某研究所将某种材料加热到1 000 ℃时停止加热，并立即将材料分为A，B两组，采用不同工艺做降温对比试验，设降温开始后经过x min时，A，B两组材料的温度分别为$y_{A}$℃，$y_{B}$℃.$y_{A}$，$y_{B}$与x的函数关系式分别为$y_{A}=kx + b$，$y_{B}=\frac{1}{4}(x - 60)^{2}+m$(部分图像如图所示)，当x=40时，两组材料的温度相同.
(1)分别求$y_{A}$，$y_{B}$关于x的函数关系式；
(2)当A组材料的温度降至120 ℃时，B组材料的温度是多少?
(3)在0＜x＜40的哪一时刻，两组材料温差最大?

答案： 解：
(1)由题意可得$y_B=\frac{1}{4}(x - 60)^2 + m$的图像过点$(0,1000)$，则$1000=\frac{1}{4}\times(0 - 60)^2 + m$，解得$m = 100$，$\therefore y_B=\frac{1}{4}\cdot(x - 60)^2 + 100$，当$x = 40$时，$y_B=\frac{1}{4}\times(40 - 60)^2 + 100$，解得$y_B = 200$，因为$y_A = kx + b$的图像经过点$(0,1000)$，$(40,200)$，则$\begin{cases}b = 1000,\\40k + b = 200,\end{cases}$解得$\begin{cases}b = 1000,\\k = - 20,\end{cases}$
$\therefore y_A=-20x + 1000$；
(2)当$A$组材料的温度降至$120^{\circ}C$时，$120=-20x + 1000$，解得$x = 44$，当$x = 44$，$y_B=\frac{1}{4}\times(44 - 60)^2 + 100 = 164(^{\circ}C)$，
$\therefore$此时$B$组材料的温度是$164^{\circ}C$；
(3)当$0\lt x\lt40$时，$y_A - y_B=-20x + 1000-\frac{1}{4}(x - 60)^2 - 100=-\frac{1}{4}x^2 + 10x=-\frac{1}{4}(x - 20)^2 + 100$，
$\therefore$当$x = 20$时，两组材料温差最大，为$100^{\circ}C$.