2025年全优课堂考点集训与满分备考九年级数学下册冀教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年全优课堂考点集训与满分备考九年级数学下册冀教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
14. 廊桥是我国古老的文化遗产.如图所示的是某座抛物线形的廊桥示意图,已知抛物线的函数表达式为$y=-\frac{1}{40}x^{2}+10$,为保护廊桥的安全,在该抛物线上距水面AB高为8 m的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF的长度.(精确到1 m)
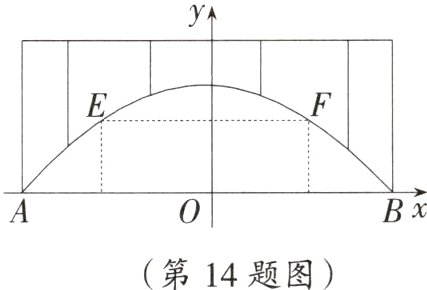

答案:
解:由“在该抛物线上距水面AB高为8m的点为E,F”把y=8代入y= - $\frac{1}{40}$x²+10,得x = ±4$\sqrt{5}$,则EF = 8$\sqrt{5}$≈18(m).
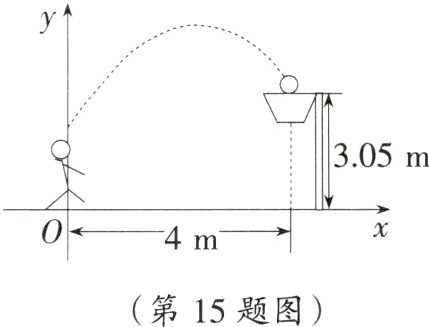
15. 如图,一位篮球运动员在离篮圈中心水平距离4 m处跳起投篮,球运行的高度y(m)与运行的水平距离x(m)满足表达式$y=ax^{2}+x+c$,当球运行的水平距离为1.5 m时,球离地面高度为3.3 m,球在空中达到最大高度后,准确落入篮圈内.已知篮圈中心离地面距离为3.05 m.
(1)当球运行的水平距离为多少时,达到最大高度?最大高度为多少?
(2)若该运动员身高1.8 m,这次跳投时,球在他头顶上方0.25 m处出手,问球出手时,他跳离地面多高?
(1)当球运行的水平距离为多少时,达到最大高度?最大高度为多少?
(2)若该运动员身高1.8 m,这次跳投时,球在他头顶上方0.25 m处出手,问球出手时,他跳离地面多高?

答案:
解:
(1)依题意,抛物线y = ax²+x+c经过点(1.5,3.3)和(4,3.05),
∴$\begin{cases}a·1.5²+1.5+c = 3.3 \\a·4²+4+c = 3.05\end{cases}$,解得$\begin{cases}a = - 0.2 \\c = 2.25\end{cases}$,
∴y = - 0.2x²+x+2.25 = - 0.2(x - 2.5)²+3.5,
∴当球运行的水平距离为2.5 m时,达到最大高度,最大高度为3.5 m;
(2)
∵x = 0时,y = 2.25,
∴2.25 - 0.25 - 1.8 = 0.2(m),即球出手时,他跳离地面0.2 m.
(1)依题意,抛物线y = ax²+x+c经过点(1.5,3.3)和(4,3.05),
∴$\begin{cases}a·1.5²+1.5+c = 3.3 \\a·4²+4+c = 3.05\end{cases}$,解得$\begin{cases}a = - 0.2 \\c = 2.25\end{cases}$,
∴y = - 0.2x²+x+2.25 = - 0.2(x - 2.5)²+3.5,
∴当球运行的水平距离为2.5 m时,达到最大高度,最大高度为3.5 m;
(2)
∵x = 0时,y = 2.25,
∴2.25 - 0.25 - 1.8 = 0.2(m),即球出手时,他跳离地面0.2 m.
16. 应用意识 如图,某公路隧道横截面为抛物线,其最大高度为6 m,底部宽度OM为12 m.现以点O为原点,OM所在直线为x轴建立平面直角坐标系.
(1)直接写出点M及抛物线顶点P的坐标;
(2)求这条抛物线的表达式;
(3)若要搭建一个矩形“支撑架”AD—DC—CB,使点C,D在抛物线上,点A,B在地面OM上,则这个“支撑架”总长的最大值是多少?
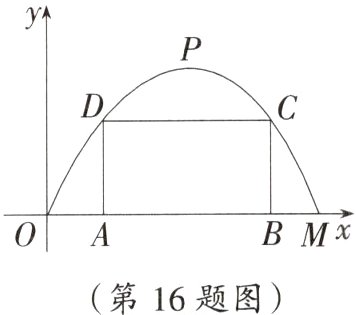
(1)直接写出点M及抛物线顶点P的坐标;
(2)求这条抛物线的表达式;
(3)若要搭建一个矩形“支撑架”AD—DC—CB,使点C,D在抛物线上,点A,B在地面OM上,则这个“支撑架”总长的最大值是多少?

答案:
解:
(1)M(12,0),P(6,6);
(2)设抛物线的表达式为y = a(x - 6)²+6,
∵抛物线y = a(x - 6)²+6经过点(0,0),
∴0 = a(0 - 6)²+6,解得a = - $\frac{1}{6}$,
∴抛物线的表达式为y = - $\frac{1}{6}$(x - 6)²+6,即y = - $\frac{1}{6}$x²+2x;
(3)设A(m,0),则B(12 - m,0),C(12 - m,- $\frac{1}{6}$m²+2m),D(m,- $\frac{1}{6}$m²+2m).
∴“支撑架”总长AD+DC+CB = (- $\frac{1}{6}$m²+2m)+(12 - 2m)+(- $\frac{1}{6}$m²+2m)= - $\frac{1}{3}$m²+2m+12 = - $\frac{1}{3}$·(m - 3)²+15.
∵此二次函数的图像开口向下,
∴当m = 3 m时,AD+DC+CB有最大值,最大值为15 m.
(1)M(12,0),P(6,6);
(2)设抛物线的表达式为y = a(x - 6)²+6,
∵抛物线y = a(x - 6)²+6经过点(0,0),
∴0 = a(0 - 6)²+6,解得a = - $\frac{1}{6}$,
∴抛物线的表达式为y = - $\frac{1}{6}$(x - 6)²+6,即y = - $\frac{1}{6}$x²+2x;
(3)设A(m,0),则B(12 - m,0),C(12 - m,- $\frac{1}{6}$m²+2m),D(m,- $\frac{1}{6}$m²+2m).
∴“支撑架”总长AD+DC+CB = (- $\frac{1}{6}$m²+2m)+(12 - 2m)+(- $\frac{1}{6}$m²+2m)= - $\frac{1}{3}$m²+2m+12 = - $\frac{1}{3}$·(m - 3)²+15.
∵此二次函数的图像开口向下,
∴当m = 3 m时,AD+DC+CB有最大值,最大值为15 m.
17. 建立函数模型法几何直观 如图所示的是把一个抛物线形桥拱,量得的两个数据,画在纸上的情形.小明说只要建立适当的坐标系,就能求出此抛物线的表达式. 你认为他的说法正确吗?如果不正确,请说明理由;如果正确,请你帮小明求出该抛物线的表达式.


答案:
解:正确.抛物线依坐标系所建不同而各异,如图,令y=ax²,代入(20,−6)得−6=a·20²,解得a=−$\frac{3}{200}$,
∴y = - $\frac{3}{200}$x².(答案不唯一)

解:正确.抛物线依坐标系所建不同而各异,如图,令y=ax²,代入(20,−6)得−6=a·20²,解得a=−$\frac{3}{200}$,
∴y = - $\frac{3}{200}$x².(答案不唯一)

查看更多完整答案,请扫码查看


