《2025年全优课堂考点集训与满分备考九年级数学下册冀教版》

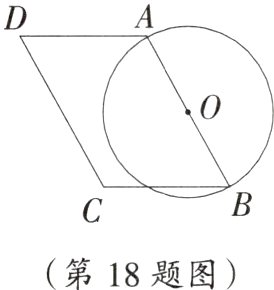
18. 如图,在□ABCD中,∠D=60°,以AB为直径作⊙O,已知AB=10,AD=m.
(1)求O到CD的距离;(用含m的代数式表示)
(2)若m=6,通过计算判断⊙O与CD的位置关系;
(3)若⊙O与线段CD所在直线有一个公共点,求m的值.

答案： 解：
(1)根据平行线间的距离相等，得O到CD的距离等于A到CD的距离. 根据∠D = 60°，AD = m，得O到CD的距离是$\frac{\sqrt{3}}{2}$m；
(2)
∵AB = 10，
∴⊙O的半径为$\frac{1}{2}$AB = 5，当m = 6时，$\frac{\sqrt{3}}{2}$m = 3$\sqrt{3}$＞5，故⊙O与CD的位置关系是相离；
(3)若⊙O与线段CD所在直线有一个公共点，则CD所在直线与⊙O相切，即$\frac{\sqrt{3}}{2}$m = 5，解得m = $\frac{10\sqrt{3}}{3}$.

19. [应用意识] 如图,已知点O为原点,点A的坐标为(4,3),⊙A的半径为2.过点A作直线l平行于x轴,交y轴于点B,点P在直线l上运动.
(1)当点P在⊙A上时,直接写出它的坐标;
(2)设点P的横坐标为12,试判断直线OP与⊙A的位置关系,并说明理由.(参考数据：$\sqrt{153}$ ≈12.37)

答案： 解：
(1)点P的坐标是(2，3)或(6，3)；
(2)如图，连接OP，过点A作AC⊥OP，垂足为C. 那么AP = PB - AB = 12 - 4 = 8，OB = 3，OP = $\sqrt{12^{2}+3^{2}}$ = $\sqrt{153}$.
∵∠ACP = ∠OBP = 90°，∠1 = ∠1，
∴△APC∽△OPB.
∴$\frac{AC}{OB}$ = $\frac{AP}{OP}$.
∴$\frac{AC}{3}$ = $\frac{8}{\sqrt{153}}$.
∴AC = $\frac{24}{\sqrt{153}}$≈1.9＜2，
∴直线OP与⊙A相交.

20. [材料阅读法推理能力] 已知平面直角坐标系中点P(x₀,y₀)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式d=|kx₀-y₀+b|/$\sqrt{1+k²}$计算.
例如:求点P(-1,2)到直线y=3x+7的距离.
因为直线y=3x+7,其中k=3,b=7,所以点P(-1,2)到直线y=3x+7的距离为d=|kx₀-y₀+b|/$\sqrt{1+k²}$=|3×(-1)-2+7|/$\sqrt{1+3²}$=$\frac{2}{\sqrt{10}}$=$\frac{\sqrt{10}}{5}$.据此解答下列问题.
(1)求点P(1,-3)到直线y=x-1的距离;
(2)已知圆心Q坐标为(0,5),半径r为3,判断⊙Q与直线y=$\sqrt{3}$ x+9的位置关系并说明理由.

答案： 解：
(1)点P(1，-3)到直线y = x - 1的距离为$\frac{|1×1 + 3 - 1|}{\sqrt{1 + 1^{2}}}$ = $\frac{3\sqrt{2}}{2}$；
(2)⊙Q与直线y = $\sqrt{3}$x + 9的位置关系为相交. 理由如下：圆心Q(0，5)到直线y = $\sqrt{3}$x + 9的距离为d = $\frac{|\sqrt{3}×0 - 5 + 9|}{\sqrt{1 + (\sqrt{3})^{2}}}$ = $\frac{4}{2}$ = 2.
∵⊙Q的半径r = 3，
∴d＜r，
∴⊙Q与直线y = $\sqrt{3}$x + 9相交.