《2025年阳光夺冠九年级数学下册》

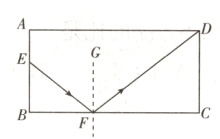
22.(10分)如图，矩形ABCD为台球桌面，AD = 260 cm，AB = 130 cm，球目前在E点位置，AE = 60 cm. 如果小丁瞄准BC边上的点F将球打过去，经过反弹后，球刚好弹到D点位置.
(1)求证：△BEF∽△CDF；
(2)求CF的长.

答案：
(1)证明：由球的反弹，可知$\angle EFG = \angle GFD$.
∵$GF\perp BC$，
∴$\angle BFE = \angle CFD$.
又
∵$\angle B = \angle C = 90^{\circ}$，
∴$\triangle BEF\sim\triangle CDF$；
(2)$CF$的长是169 cm.

23.(10分)如图，一条河的两岸有一段是平行的，在河的南岸边每隔5米有一棵树，在北岸边每隔50米有一根电线杆. 小丽站在离南岸边15米的点P处看北岸，发现北岸相邻的两根电线杆A，B恰好被南岸的两棵树C，D遮住，并且在这两棵树之间还有三棵树，求河的宽度.

答案：
解：过点P作$PF\perp AB$，交CD于点E，交AB于点F.
设河宽为x米.
∵$AB// CD$，
∴$\angle PDC = \angle PBA$，$\angle PCD = \angle PAB$，
∴$\triangle PDC\sim\triangle PBA$，
∴$\frac{CD}{AB}=\frac{PE}{PF}$，
∴$\frac{CD}{AB}=\frac{15}{15 + x}$.
依题意，易得$CD = 20$米，$AB = 50$米，
∴$\frac{20}{50}=\frac{15}{15 + x}$，解得$x = 22.5$.
答：河的宽度为22.5米. 

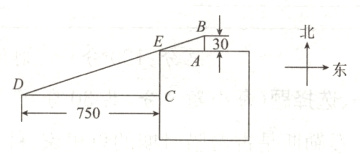
24.(10分)我国古代数学著作《九章算术》中记载了一个问题：“今有邑方不知大小，各开门，出北门三十步有木，出西门七百五十步见木，问：邑方几何?”其大意如下：如图，一座正方形城池在各边的中点开门，A为北门的中点，出北门往正北方向30步(“步”为古代的长度单位)，有一棵树木(点B)，C为西门的中点，出西门往正西方向走750步到D处正好看到B处的树木，问：正方形城池的边长为多少步？请你用所学知识解决这个问题.

答案： 解：由题意，得$\angle BAE = \angle ECD = 90^{\circ}$，$BA// EC$，
∴$\angle B = \angle DEC$，
∴$\triangle BAE\sim\triangle ECD$，
∴$\frac{AE}{CD}=\frac{BA}{EC}$.
设正方形城池的边长为x步，则$\frac{\frac{x}{2}}{750}=\frac{30}{\frac{x}{2}}$，解得$x_1 = 300$，$x_2 = - 300$(舍去).
答：正方形城池的边长为300步.