《2025年教材帮高中数学选择性必修第二册苏教版》

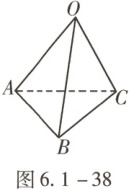
7. (2025·天津市南开区质检)如图6.1-38,在四面体OABC中,OA=8,AB=6,AC=4,BC=5,$\angle OAC=45°$,$\angle OAB=60°$,则异面直线OA与BC的夹角的余弦值为$\frac{3 - 2\sqrt{2}}{5}$.

答案： 7.$\frac{3 - 2\sqrt{2}}{5}$
∵$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$，
∴$\overrightarrow{OA}·\overrightarrow{BC}=\overrightarrow{OA}·\overrightarrow{AC}-\overrightarrow{OA}·\overrightarrow{AB}=|\overrightarrow{OA}|·|\overrightarrow{AC}|·\cos\langle\overrightarrow{OA},\overrightarrow{AC}\rangle-|\overrightarrow{OA}|·|\overrightarrow{AB}|·\cos\langle\overrightarrow{OA},\overrightarrow{AB}\rangle=8×4×\cos135^{\circ}-8×6×\cos120^{\circ}=24 - 16\sqrt{2}$。\n
∴$\cos\langle\overrightarrow{OA},\overrightarrow{BC}\rangle=\frac{\overrightarrow{OA}·\overrightarrow{BC}}{|\overrightarrow{OA}|·|\overrightarrow{BC}|}=\frac{24 - 16\sqrt{2}}{8×5}=\frac{3 - 2\sqrt{2}}{5}$，\n故异面直线OA与BC的夹角的余弦值为$\frac{3 - 2\sqrt{2}}{5}$。

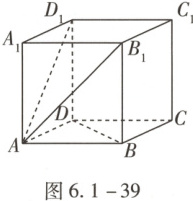
例25 (2024·上海改编)如图6.1-39,已知四棱柱$ABCD-A_1B_1C_1D_1$,底面ABCD为平行四边形,$AA_1=3$,BD=4,且$\overrightarrow{AB_1}·\overrightarrow{BC}-\overrightarrow{AD_1}·\overrightarrow{DC}=5$,则异面直线$AA_1$与BD夹角的余弦值为.

答案： 解析 令$\overrightarrow{AB}=\boldsymbol{a}$,$\overrightarrow{AD}=\boldsymbol{b}$,$\overrightarrow{AA_1}=\boldsymbol{c}$,则$\overrightarrow{AB_1}·\overrightarrow{BC}-\overrightarrow{AD_1}·\overrightarrow{DC}=(\overrightarrow{AB}+\overrightarrow{BB_1})·\overrightarrow{BC}-(\overrightarrow{AD}+\overrightarrow{DD_1})·\overrightarrow{DC}=(\boldsymbol{a}+\boldsymbol{c})·\boldsymbol{b}-(\boldsymbol{b}+\boldsymbol{c})·\boldsymbol{a}=\boldsymbol{c}·(\boldsymbol{b}-\boldsymbol{a})=\overrightarrow{AA_1}·\overrightarrow{BD}=|\overrightarrow{AA_1}|·|\overrightarrow{BD}|·\cos\langle\overrightarrow{AA_1},\overrightarrow{BD}\rangle=5$,所以$\cos\langle\overrightarrow{AA_1},\overrightarrow{BD}\rangle=\dfrac{5}{12}$.
答案 $\dfrac{5}{12}$

例26 (浙江高考题)如图6.1-40,已知平面四边形ABCD,AB=BC=3,CD=1,AD=$\sqrt{5}$,$\angle ADC=90°$.沿直线AC将△ACD翻折成$\triangle ACD'$,直线AC与$BD'$所成角的余弦的最大值是.

答案：
解析 如图6.1-41,过点$D'$作$D'F\perp AC$于点F,取AC的中点E,连接BE,则AC⊥BE.

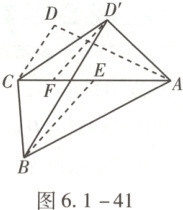
在$\triangle AD'C$中,
∵ $\angle AD'C=90°$,$CD'=1$,$AD'=\sqrt{5}$,
∴ AC=$\sqrt{6}$,
∴ $D'F=\dfrac{1×\sqrt{5}}{\sqrt{6}}=\dfrac{\sqrt{30}}{6}$,
∴ CF=$\sqrt{D'C^2-D'F^2}=\dfrac{\sqrt{6}}{6}$,
∴ EF=$\dfrac{\sqrt{6}}{2}-\dfrac{\sqrt{6}}{6}=\dfrac{\sqrt{6}}{3}$.
BE=$\sqrt{BC^2-CE^2}=\dfrac{\sqrt{30}}{2}$.
$\overrightarrow{BD'}=\overrightarrow{BE}+\overrightarrow{EF}+\overrightarrow{FD'}$,
则$\overrightarrow{BD'}·\overrightarrow{AC}=(\overrightarrow{BE}+\overrightarrow{EF}+\overrightarrow{FD'})·\overrightarrow{AC}=\overrightarrow{EF}·\overrightarrow{AC}=\dfrac{\sqrt{6}}{3}×\sqrt{6}=2$.
设AC与$BD'$所成的角为θ,
又$|\overrightarrow{BD'}|^2=(\overrightarrow{BE}+\overrightarrow{EF}+\overrightarrow{FD'})^2=\dfrac{30}{4}+\dfrac{6}{9}+\dfrac{30}{36}+2×\dfrac{\sqrt{30}}{2}×\dfrac{\sqrt{30}}{6}·\cos\langle\overrightarrow{BE},\overrightarrow{FD'}\rangle=9+5\cos\langle\overrightarrow{BE},\overrightarrow{FD'}\rangle$,$|\overrightarrow{AC}|=\sqrt{6}$,则$\cos\theta=\left|\dfrac{\overrightarrow{BD'}·\overrightarrow{AC}}{|\overrightarrow{BD'}|·|\overrightarrow{AC}|}\right|=\dfrac{2}{\sqrt{9+5\cos\langle\overrightarrow{BE},\overrightarrow{FD'}\rangle}·\sqrt{6}}$,
故当$\cos\langle\overrightarrow{BE},\overrightarrow{FD'}\rangle=-1$,即点$D'$在平面ABC内时,$\cos\theta$取得最大值,为$\dfrac{\sqrt{6}}{6}$.
答案 $\dfrac{\sqrt{6}}{6}$
考向2 利用向量法解决空间位置问题