《2025年教材帮高中数学选择性必修第二册苏教版》

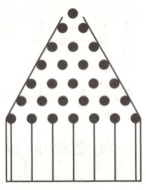
2.[多选题](2025·福建省莆田第一中学入学考试)如图8.2.3-2是一块高尔顿板示意图，在一块木块上钉着若干排相互平行但相互错开的圆柱形小木钉，小木钉之间留有适当的空隙作为通道，前面挡有一块玻璃，将小球从顶端放入，小球在下落过程中，每次碰到小木钉后都等可能地向左或向右落下，最后落入底部的格子中，格子从左到右分别编号为0,1,2,3,4,5，用X表示小球最后落入格子的号码，则下面计算正确的是(ACD)

A.P(X=0)=$\frac{1}{32}$
B.P(X=5)=$\frac{1}{64}$
C.E(X)=$\frac{5}{2}$
D.D(X)=$\frac{5}{4}$

答案： 2.ACD 设$A=$“向右下落”，则$\overline{A}=$“向左下落”，$P(A)=P(\overline{A})=\frac{1}{2}$，因为小球最后落人格子的号码$X$等于事件$A$发生的次数，而
小球下落的过程中共碰撞小木钉$5$次，所以$X\sim B(5,\frac{1}{2})$，
对于$A$，$P(X=0)=(\frac{1}{2})^5=\frac{1}{32}$，故$A$正确；
对于$B$，$P(X=5)=(\frac{1}{2})^5=\frac{1}{32}$，故$B$错误；
对于$C$，$E(X)=5×\frac{1}{2}=\frac{5}{2}$，故$C$正确；
对于$D$，$D(X)=5×\frac{1}{2}×(1-\frac{1}{2})=\frac{5}{4}$，故$D$正确.

例10 某一批产品的合格率为95%，那么在取出的20件产品中，最有可能有几件产品合格？

答案： 解析 设在取出的20件产品中，合格产品有X件，则X~B(20,0.95)，
于是恰好有k件产品合格的概率为P(X=k)=$C_{20}^k×0.95^k×0.05^{20-k}$(0≤k≤20且k∈N).
∵$\frac{P(X=k)}{P(X=k-1)}=\frac{C_{20}^k×0.95^k×0.05^{20-k}}{C_{20}^{k-1}×0.95^{k-1}×0.05^{21-k}}=\frac{(20-k+1)×0.95}{k×0.05}=1+\frac{21×0.95-k}{k×0.05}=1+\frac{19.95-k}{k×0.05}$(1≤k≤20且k∈N).
(目的是比较比值与1的大小关系)
于是当k＜19.95时，P(X=k-1)＜P(X=k)，
当k＞19.95时，P(X=k-1)＞P(X=k).
由以上分析可知，在取出的20件产品中，合格品有19件的概率最大，即最有可能有19件合格品.

例11 (2025·四川省大数据精准教学联盟一模)甲、乙两名同学进行定点投篮训练，据以往训练数据分析，甲每次投篮命中的概率为$\frac{2}{3}$，乙每次投篮命中的概率为$\frac{1}{2}$，每次投篮互不影响.现甲、乙两人开展多轮次的定点投篮活动，每轮次各投2个球，每投进一个球记1分，未投进记-1分.
(1)求甲在一轮投篮结束后的得分不大于0的概率.
(2)记甲、乙每轮投篮得分之和为X.
①求X的分布列和数学期望；
②若X＞0，则称该轮次为一个“成功轮次”.在连续n(n≥8)轮次的投篮活动中，记“成功轮次”的次数为Y，当n为何值时，P(Y=8)的值最大？

答案：
解析
(1)甲在一轮投篮结束后的得分不大于0，即甲在一轮投篮中至多命中一次，
所以甲在一轮投篮结束后的得分不大于0的概率为P=1-$(\frac{2}{3})^2=\frac{5}{9}$.（正难则反，先求“甲在一轮投篮中命中两次”的概率，再用对立事件的概率公式求解）
(2)①由题知X可能取值为-4,-2,0,2,4，
P(X=-4)=$\frac{1}{3}×\frac{1}{3}×\frac{1}{2}×\frac{1}{2}=\frac{1}{36}$，
P(X=-2)=$\frac{1}{3}×\frac{1}{3}×C_2^1(\frac{1}{2})^2+C_2^1×\frac{2}{3}×\frac{1}{3}×(\frac{1}{2})^2=\frac{1}{6}$，
P(X=0)=$\frac{1}{3}×\frac{1}{3}×\frac{1}{2}×\frac{1}{2}+C_2^1×\frac{2}{3}×\frac{1}{3}×C_2^1(\frac{1}{2})^2+\frac{2}{3}×\frac{2}{3}×\frac{1}{2}×\frac{1}{2}=\frac{13}{36}$，
P(X=2)=$\frac{2}{3}×\frac{2}{3}×C_2^1(\frac{1}{2})^2+C_2^1×\frac{2}{3}×\frac{1}{3}×(\frac{1}{2})^2=\frac{1}{3}$，
P(X=4)=$(\frac{2}{3})^2×(\frac{1}{2})^2=\frac{1}{9}$，
所以X的分布列为

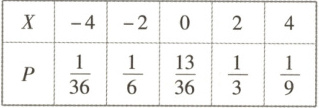
数学期望E(X)=(-4)×$\frac{1}{36}$+(-2)×$\frac{1}{6}$+0×$\frac{13}{36}$+2×$\frac{1}{3}$+4×$\frac{1}{9}$=$\frac{2}{3}$.
②由①知P(X＞0)=$\frac{1}{3}+\frac{1}{9}=\frac{4}{9}$，由题知Y~B(n,$\frac{4}{9}$)，（解题的关键点）
所以P(Y=k)=$C_n^k(\frac{4}{9})^k(1-\frac{4}{9})^{n-k}$(0≤k≤n,k∈N).由$\left\{ \begin{array}{l} P(Y=k)\geq P(Y=k-1),\\ P(Y=k)\geq P(Y=k+1), \end{array} \right.$
得$\left\{ \begin{array}{l} C_n^k(\frac{4}{9})^k(1-\frac{4}{9})^{n-k}\geq C_n^{k-1}(\frac{4}{9})^{k-1}(1-\frac{4}{9})^{n+1-k},\\ C_n^k(\frac{4}{9})^k(1-\frac{4}{9})^{n-k}\geq C_n^{k+1}(\frac{4}{9})^{k+1}(1-\frac{4}{9})^{n-k-1}, \end{array} \right.$
整理得$\left\{ \begin{array}{l} 4C_n^k\geq5C_n^{k-1},\\ 5C_n^k\geq4C_n^{k+1}, \end{array} \right.$
即$\left\{ \begin{array}{l} 4×\frac{n!}{k!(n-k)!}\geq5×\frac{n!}{(k-1)!(n-k+1)!},\\ 5×\frac{n!}{k!(n-k)!}\geq4×\frac{n!}{(k+1)!(n-k-1)!}, \end{array} \right.$
得$\left\{ \begin{array}{l} 4(n-k+1)\geq5k,\\ 5(k+1)\geq4(n-k), \end{array} \right.$
所以$\frac{4n-5}{9}\leq k\leq\frac{4n+4}{9}$.
由题知k=8，所以$\frac{4n-5}{9}\leq8\leq\frac{4n+4}{9}$，得17≤n≤$\frac{77}{4}$，
又n∈N*，所以n=17或18或19.