《2025年课时练人民教育出版社八年级数学上册人教版》

3. 计算：$2a(a - 1)-2a^{2}=$(D)

A.$a$
B.$-a$
C.$2a$
D.$-2a$

答案： 3.D

4. 先化简，再求值：$5a(3a^{2}b - ab^{2})-4a(-ab^{2}+3a^{2}b)-(3ab)^{2}$，其中 $a = -2$，$b = 3$.

答案： 解：
$\begin{aligned}&5a(3a^{2}b - ab^{2})-4a(-ab^{2}+3a^{2}b)-(3ab)^{2}\\=&15a^{3}b - 5a^{2}b^{2}+4a^{2}b^{2}-12a^{3}b - 9a^{2}b^{2}\\=&(15a^{3}b - 12a^{3}b)+(-5a^{2}b^{2}+4a^{2}b^{2}-9a^{2}b^{2})\\=&3a^{3}b - 10a^{2}b^{2}\end{aligned}$
当$a = -2$，$b = 3$时，
$\begin{aligned}&3×(-2)^{3}×3 - 10×(-2)^{2}×3^{2}\\=&3×(-8)×3 - 10×4×9\\=&-72 - 360\\=&-432\end{aligned}$
所以，原式的值为$-432$。

突破点三 多项式乘多项式
【例3】若 $(x^{2}+mx + n)(x^{2}-3x + 4)$ 的计算结果中不含 $x^{3}$ 项和 $x^{2}$ 项，试求 $m$，$n$ 的值.
思路分析
思考：在多项式乘多项式的积中，若不含某一项，则说明合并同类项之后，这一项的系数是 0.
解：

答案： 思路分析
思考:0
解:m=3,n=5.

(改变条件)若条件“计算结果中不含 $x^{3}$ 项和 $x^{2}$ 项”变为“计算结果中不含 $x^{3}$ 项和 $x$ 项”，求 $m$，$n$ 的值.
【规律方法】
(1) 运算中不要漏乘任何一项.
(2) 多项式中每一项都包含它前面的符号，确定积中每一项的符号至关重要.
(3) 多项式相乘的计算结果中不含某一项，可得合并同类项后该项的系数为0，由此可构造方程（或方程组）.

答案： 解:m=3,n=4.

5. 已知 $(x - 2)(x^{2}+mx + n)$ 的乘积中不含 $x^{2}$ 项，则 $m$ 的值为(A)

A.$2$
B.$3$
C.$-2$
D.$-3$

答案： 5.A

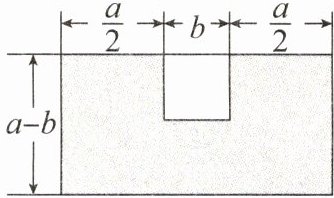
6. 某校校庆活动搭建的舞台如图所示（阴影部分，空白部分为正方形），求这个舞台的面积.

答案： 1. 首先，计算大长方形的面积：
大长方形的长为$\frac{a}{2}+b+\frac{a}{2}=a + b$，宽为$a - b$。
根据长方形面积公式$S = 长×宽$，大长方形面积$S_1=(a + b)(a - b)$。
由平方差公式$(m + n)(m - n)=m^{2}-n^{2}$，这里$m = a$，$n = b$，所以$S_1=a^{2}-b^{2}$。
2. 然后，计算空白正方形的面积：
空白正方形的边长为$b$，根据正方形面积公式$S = 边长×边长$，空白正方形面积$S_2=b× b=b^{2}$。
3. 最后，计算舞台（阴影部分）的面积：
舞台面积$S=S_1 - S_2$。
把$S_1=a^{2}-b^{2}$，$S_2 = b^{2}$代入得：$S=(a^{2}-b^{2})-b^{2}$。
化简$S=a^{2}-b^{2}-b^{2}=a^{2}-2b^{2}$。
所以这个舞台的面积是$a^{2}-2b^{2}$。