《2025年课时练人民教育出版社八年级数学上册人教版》

观察下面四幅图片。
问题 1：图①剪纸中的蝴蝶、图②中的三角形和正方形、图③电扇的叶片、图④两个五角星的共同特点是形状、大小相同。
问题 2：问题 1 中所列举的各个图中一样的图形各自放在一起能够完全重合。

答案： 形状 大小 重合

1. 全等形：能够完全重合的两个图形。

答案： 完全重合

2. 全等三角形：能够完全重合的两个三角形。

答案： 完全重合

3. 全等的表示方法：全等用符号“≌”表示，读作“全等于”，如△ABC 和△DEF 全等，记作△ABC≌△DEF。

答案： ≌ 全等于 △ABC≌△DEF

4. 全等三角形的对应元素
把两个全等的三角形重合到一起，重合的顶点叫作对应顶点，重合的边叫作对应边，重合的角叫作对应角。
学习任务二 全等三角形的性质
全等三角形的对应边相等，全等三角形的对应角相等。

答案： 重合 重合 重合 相等 相等

【例 1】如图所示，△ABC≌△EDA，∠BAC 与∠DEA 是对应角，AB 与 ED 是对应边，写出其他对应边及对应角。

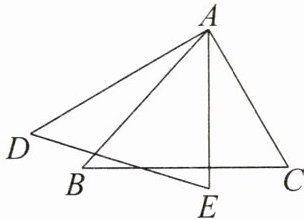
解：
【规律方法】
寻找全等三角形对应边、对应角的方法
（1）图形特征法
最长边对最长边，最短边对最短边；
最大角对最大角，最小角对最小角。
（2）位置关系法
①公共角（或对顶角）为对应角、公共边为对应边。
②对应角的对边为对应边，对应边的对角为对应角。

答案： 其他对应边:BC与DA,AC与EA.其他对应角:∠ACB与∠EAD,∠CBA与∠ADE.