《2025年课时练人民教育出版社八年级数学上册人教版》

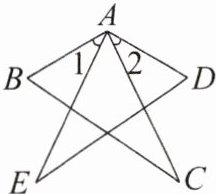
1. 如图，$AC = AE$，$\angle C = \angle E$，$\angle 1 = \angle 2$. 求证：$\triangle ABC \cong \triangle ADE$.

答案： 1.证明:因为∠1=∠2,
所以∠1+∠EAC=∠2+∠EAC,
所以∠BAC=∠DAE.
在△ABC和△ADE中,$\begin{cases} \angle BAC = \angle DAE, \\ AC = AE, \\ \angle C = \angle E, \end{cases}$
所以△ABC≌△ADE(ASA).

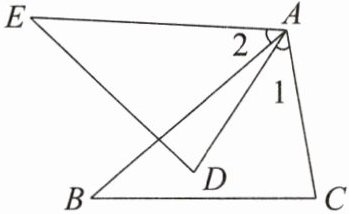
2. 如图，$AB = AE$，$\angle 1 = \angle 2$，$\angle B = \angle E$. 求证：$BC = ED$.

答案： 2.证明:因为∠1=∠2,
所以∠1+∠BAD=∠2+∠BAD,
即∠BAC=∠EAD.
在△ABC和△AED中,$\begin{cases} \angle BAC = \angle EAD, \\ AB = AE, \\ \angle B = \angle E, \end{cases}$
所以△ABC≌△AED(ASA).
所以BC=ED.

突破点二 用“AAS”判定三角形全等
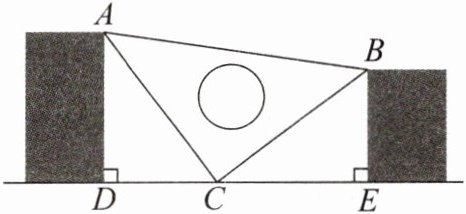
【例2】如图，三角尺$ABC$放到两个物体之间，且$AC = BC$，$AD \perp DE$，$BE \perp DE$. 求证：$\triangle ADC \cong \triangle CEB$.

思路分析
思考1：在$\triangle ADC$和$\triangle CEB$中，已知相等的边、角有哪些？
思考2：$\angle ACD$和$\angle DAC$有什么关系？$\angle ACD$和$\angle BCE$呢？
思考3：$\angle BCE$和$\angle DAC$相等吗？为什么？
证明：
【规律方法】
证明三角形全等寻找等角的方法
（1）公共角相等、对顶角相等、直角都相等；
（2）等角加（或减）等角，其和（或差）相等；
（3）同角或等角的余（补）角相等；
（4）根据角平分线、平行线找等角.

答案： 思路分析
思考1:AC=BC,∠ADC=∠CEB=90°.
思考2:∠ACD和∠DAC互余,∠ACD和∠BCE互余.
思考3:相等.因为同角的余角相等.
证明:由题意,知AC=BC,∠ACB=90°,
AD⊥DE,BE⊥DE,
所以∠ADC=∠CEB=90°,
所以∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
所以∠BCE=∠DAC.
在△ADC和△CEB中,$\begin{cases} \angle ADC = \angle CEB, \\ \angle DAC = \angle ECB, \\ AC = CB, \end{cases}$
所以△ADC≌△CEB(AAS).