第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
3. 如图,已知 AE 为△ABC 的中线,AB = 8 cm,AC = 6 cm,△ACE 的周长为 16 cm,则△ABE 的周长为
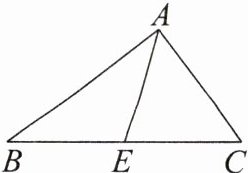
18
cm。
答案:
18
4. 如图,在△ABC 中,已知点 D,E,F 分别为 BC,AD,CE 的中点,且 $ S_{△ABC} = 8 \, cm^2 $,求阴影部分的面积。
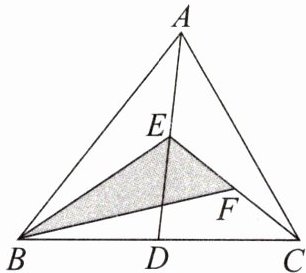

答案:
解:2 cm².
利用三角形的中线巧求面积
某数学兴趣小组探究中线在求图形面积中的作用。
【知识准备】
中线把三角形分成两个面积相等的三角形,如图,BD 为△ABC 的中线,则 $ S_{△ABD} = $
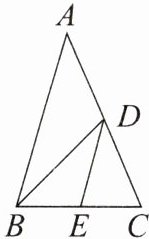
【扩展三角形】
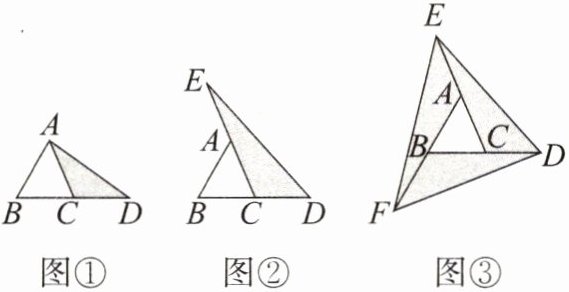
(1)如图①,$ S_{△ABC} = a $,延长 BC 到 D,使 CD = BC,连接 AD,则 $ S_{△ACD} = $
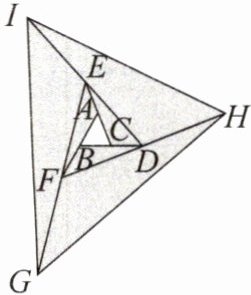
(2)像上面那样,将△ABC 各边均顺次延长一倍,连接所得端点,得到△DEF(如图③),此时,我们称△ABC 向外扩展了一次。可以发现,扩展一次后得到的△DEF 的面积是原来△ABC 面积的
【应用】
去年在面积为 10 $ m^2 $ 的△ABC 空地上栽种了某种花卉,今年把△ABC 向外进行两次扩展,第一次由△ABC 扩展成△DEF,第二次由△DEF 扩展成△IGH(如图),求这两次扩展的区域(即阴影部分)面积为多少平方米。
某数学兴趣小组探究中线在求图形面积中的作用。
【知识准备】
中线把三角形分成两个面积相等的三角形,如图,BD 为△ABC 的中线,则 $ S_{△ABD} = $
S△BDC
= $\frac{1}{2}$S△ABC
。若 DE 为△BCD 的中线,则 $ S_{△BDE} = $S△DCE
=$\frac{1}{2}$
$ S_{△BDC} = $$\frac{1}{4}$
$ S_{△ABC} $。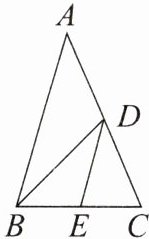
【扩展三角形】
(1)如图①,$ S_{△ABC} = a $,延长 BC 到 D,使 CD = BC,连接 AD,则 $ S_{△ACD} = $
a
。如图②,$ S_{△ABC} = a $,延长 BC 到 D,使 CD = BC,延长 CA 到 E,使 AE = AC,连接 DE,则 $ S_{△ECD} = $2a
。在图②的基础上延长 AB 到点 F,使 BF = AB,连接 FD,FE,得到△DEF(如图③),则阴影部分的面积为6a
。(以上三空均用含 a 的代数式填写)(2)像上面那样,将△ABC 各边均顺次延长一倍,连接所得端点,得到△DEF(如图③),此时,我们称△ABC 向外扩展了一次。可以发现,扩展一次后得到的△DEF 的面积是原来△ABC 面积的
7
倍。【应用】
去年在面积为 10 $ m^2 $ 的△ABC 空地上栽种了某种花卉,今年把△ABC 向外进行两次扩展,第一次由△ABC 扩展成△DEF,第二次由△DEF 扩展成△IGH(如图),求这两次扩展的区域(即阴影部分)面积为多少平方米。


答案:
【知识准备】
S△BDC S△ABC S△DCE $\frac{1}{2}$ $\frac{1}{4}$
【扩展三角形】
(1)a 2a 6a
(2)7
【应用】
两次扩展区域(即阴影部分)的面积为480 m².
S△BDC S△ABC S△DCE $\frac{1}{2}$ $\frac{1}{4}$
【扩展三角形】
(1)a 2a 6a
(2)7
【应用】
两次扩展区域(即阴影部分)的面积为480 m².
查看更多完整答案,请扫码查看


