《2025年三维数字课堂八年级数学上册人教版》

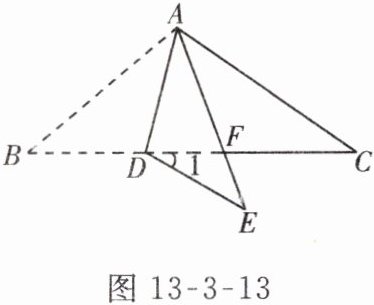
6. 如图 13 - 3 - 13,在 $ \triangle ABC $ 中,$ D $ 为 $ BC $ 上一点,将 $ \triangle ABD $ 沿 $ AD $ 翻折得到 $ \triangle AED $,$ AE $ 与 $ BC $ 相交于点 $ F $,若 $ AE $ 平分 $ \angle CAD $,$ \angle B = 40^{\circ} $,$ \angle C = 35^{\circ} $.
(1) 求证 $ \angle CAF = \angle C $；
(2) 求 $ \angle 1 $ 的度数.

答案：
(1)证明:
∵∠B=40°,∠C=35°,
∴∠BAC=180°-40°-35°=105°.
∵AE平分∠CAD,
∴∠CAF=∠DAF.
由翻折,可知∠BAD=∠DAF,
∴∠CAF=∠DAF=∠BAD,
∴∠CAF=1/3∠BAC=35°,
∴∠CAF=∠C.
(2)解:
∵∠CAF=∠C=35°,
∴∠AFC=180°-35°-35°=110°.
∵∠AFC=∠DFE,∠E=∠B=40°,
∴∠1=180°-110°-40°=30°.

7. 【推理能力】如图 13 - 3 - 14 所示,$ \triangle ABC $ 的角平分线 $ BD $,$ CE $ 相交于点 $ P $.
(1) 若 $ \angle ABC = 50^{\circ} $,$ \angle ACB = 70^{\circ} $,则 $ \angle A = $______$^{\circ} $.
(2) 试猜想 $ \angle DPC $ 与 $ \angle A $ 之间的数量关系,并说明理由.

答案：
(1)60
(2)∠DPC=90°-1/2∠A.理由:
∵∠ABC,∠ACB的平分线相交于点P,
∴∠1=1/2∠ABC,∠2=1/2∠ACB,
∴∠BPC=180°-∠1-∠2=180°-1/2∠ABC-1/2∠ACB=180°-1/2(∠ABC+∠ACB).
∵∠ABC+∠ACB=180°-∠A,
∴∠BPC=180°-1/2(180°-∠A)=90°+1/2∠A,
∴∠DPC=180°-(90°+1/2∠A)=90°-1/2∠A.

材料阅读：如图 13 - 3 - 15①所示的图形,像我们常见的学习用品——圆规. 我们不妨把这样的图形叫作“规形图”.
(1) 观察图 13 - 3 - 15①,试探究 $ \angle BDC $ 与 $ \angle A $,$ \angle B $,$ \angle C $ 之间的数量关系,并说明理由.
(2) 请你直接利用以上结论,解决以下两个问题：
Ⅰ. 如图 13 - 3 - 15②,把一块三角尺 $ DEF $ 放置在 $ \triangle ABC $ 上,使三角尺的两条直角边 $ DE $,$ DF $ 恰好分别经过点 $ B $,$ C $,若 $ \angle A = 40^{\circ} $,则 $ \angle ABD + \angle ACD = $______$^{\circ} $；
Ⅱ. 如图 13 - 3 - 15③,$ BD $ 平分 $ \angle ABP $,$ CD $ 平分 $ \angle ACP $,若 $ \angle A = 40^{\circ} $,$ \angle BPC = 130^{\circ} $,求 $ \angle BDC $ 的度数.

答案：
(1)∠BDC=∠A+∠B+∠C.
理由:连接BC,由三角形的内角和是180°,得∠A+∠ABC+∠ACB=180°,∠BDC+∠DBC+∠DCB=180°,
∴∠BDC=180°-∠DBC-∠DCB.
∵∠ABC=∠ABD+∠DBC,∠ACB=∠ACD+∠DCB,
∴∠A+∠ABD+∠DBC+∠ACD+∠DCB=180°,
∴∠A+∠ABD+∠ACD=180°-∠DBC-∠DCB.
∴∠BDC=∠A+∠ABD+∠ACD.
(2)Ⅰ.50
Ⅱ.由
(1)得∠BPC=∠A+∠ABP+∠ACP,∠BDC=∠A+∠ABD+∠ACD,
∴∠ABP+∠ACP=∠BPC-∠A=130°-40°=90°.
又
∵BD平分∠ABP,CD平分∠ACP,
∴∠ABD+∠ACD=1/2(∠ABP+∠ACP)=45°.
∴∠BDC=40°+45°=85°.