《2025年三维数字课堂八年级数学上册人教版》

1. 在①$(x + 1)(1 + x)$,②$(\frac{1}{2}a + b)(b - \frac{1}{2}a)$,③$(-a + b)(a - b)$,④$(x^2 - y)(x + y^2)$,⑤$(-a - b)(a - b)$,⑥$(c^2 - d^2)(d^2 + c^2)$中,能用平方差公式计算的有( )

A.$3$个
B.$4$个
C.$5$个
D.$6$个

答案： A

2. 若$x^2 - y^2 = 4$,则$(x - y)^2(x + y)^2$的值为( )

A.$4$
B.$16$
C.$24$
D.$32$

答案： B

3. 对于任意正整数$n$,能整除式子$(3n + 1)·(3n - 1) - (3 - n)(3 + n)$的整数是( )

A.$3$
B.$6$
C.$10$
D.$9$

答案： C

4. 【新定义】定义：$a※b = a(b + 1)$。例如：$2※3 = 2×(3 + 1) = 2×4 = 8$,则$(x - 1)※x= $______。

答案： $x^{2}-1$

5. 已知$M = 2025^2$,$N = 2024×2026$,则$M与N$的大小关系是______。

答案： $M＞N$

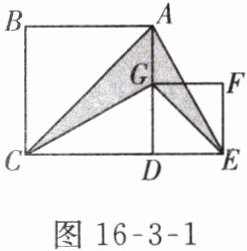
6. 如图 16 - 3 - 1 所示,大正方形与小正方形的面积之差是$64$,则阴影部分的面积是______。
]

答案： 32 点拨:由题意,知$AD^{2}-DG^{2}=64$,阴影部分面积为$\frac {1}{2}AG\cdot CD+\frac {1}{2}AG\cdot DE=\frac {1}{2}AG(CD+DE)=\frac {1}{2}(AD-DG)\cdot (AD+DG)=\frac {1}{2}(AD^{2}-DG^{2})=32.$

7. 先化简,再求值：$(2x - 3y)(3x + 2y) - (2x - y)(y + 2x)$,其中$x = 1$,$y = -2$。

答案： 解:原式$=6x^{2}+4xy-9xy-6y^{2}-(2x-y)(2x+y)=6x^{2}-5xy-6y^{2}-(4x^{2}-y^{2})=6x^{2}-5xy-6y^{2}-4x^{2}+y^{2}=2x^{2}-5xy-5y^{2}.$当$x=1,y=-2$时,原式$=2×1^{2}-5×1×(-2)-5×(-2)^{2}=-8.$

8. 某中学为了响应国家“发展体育运动,增强人民体质”的号召,决定建一个长方体游泳池,已知游泳池的长为$(4a^2 + 9b^2)m$,宽为$(2a + 3b)m$,深为$(2a - 3b)m$,这个游泳池的容积是多少？

答案： 解:$(4a^{2}+9b^{2})(2a+3b)(2a-3b)=(4a^{2}+9b^{2})(4a^{2}-9b^{2})=(16a^{4}-81b^{4})m^{3}.$答:这个游泳池的容积是$(16a^{4}-81b^{4})m^{3}.$

先观察下面的解题过程,然后解答问题：
化简：$(2 + 1)(2^2 + 1)(2^4 + 1)$。
解：原式：$=(2 - 1)(2 + 1)(2^2 + 1)(2^4 + 1)$
$=(2^2 - 1)(2^2 + 1)(2^4 + 1)$
$=(2^4 - 1)(2^4 + 1)$
$=2^8 - 1$。
化简：$(3 + 1)(3^2 + 1)(3^4 + 1)(3^8 + 1)·…·(3^{64} + 1)$。

答案： 解:原式$=\frac {1}{2}(3-1)(3+1)(3^{2}+1)(3^{4}+1)(3^{8}+1)\cdot ... \cdot (3^{64}+1)=\frac {1}{2}(3^{2}-1)(3^{2}+1)(3^{4}+1)(3^{8}+1)\cdot ... \cdot (3^{64}+1)=\frac {1}{2}(3^{4}-1)(3^{4}+1)(3^{8}+1)\cdot ... \cdot (3^{64}+1)=\frac {1}{2}(3^{8}-1)(3^{8}+1)\cdot ... \cdot (3^{64}+1)=\frac {1}{2}(3^{64}-1)(3^{64}+1)=\frac {1}{2}(3^{128}-1).$