第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
活动一 确定简单平面图形的重心位置
1. 取一块质地均匀的三角形木板,顶住三角形的某一个点,若这块木板能保持平衡,则这个点是( )
A. 三角形的一个顶点
B. 三角形的一条边的中点
C. 三角形三条中线的交点
D. 三角形三条高所在直线的交点
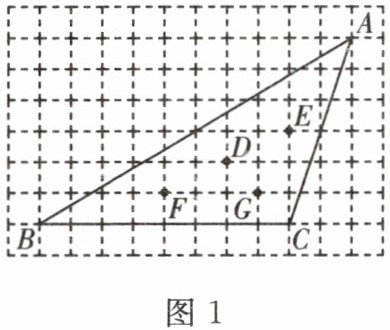
2. 如图1所示的网格由边长相同的小正方形组成,点A,B,C,D,E,F,G在小正方形的格点上,则$\triangle ABC$的重心是( )
A. 点D B. 点E C. 点F D. 点G
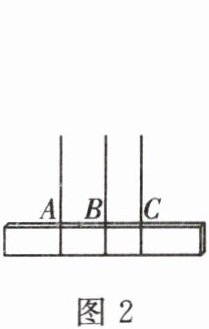
3. 如图2,乐乐用细线绑一块木板,然后提着细线使木板悬空. 乐乐发现,当将细线在A,C处捆绑木板时,木板不能水平悬空,而将细线在B处捆绑时,木板能水平悬空,则可以确定木板的重心在____处.
4. 通过查阅资料和使用悬挂法测定可知,线段的重心是____,正方形的重心是____,长方形的重心是____,平行四边形的重心是____,圆的重心是____.
活动二 确定平面组合图形的重心位置
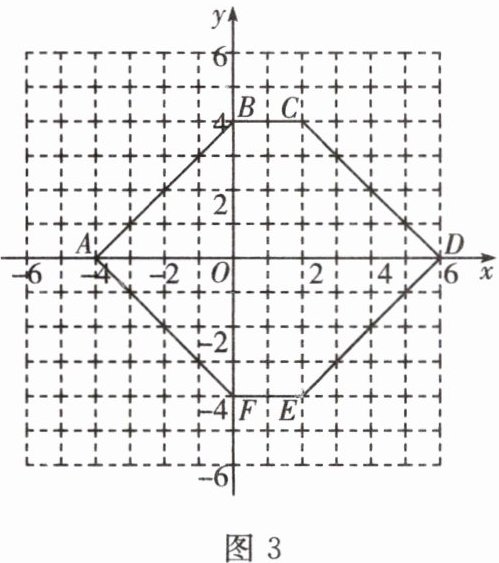
5. 如图3,根据多边形ABCDEF在平面直角坐标系中的位置,可以确定这个多边形的重心坐标为____.
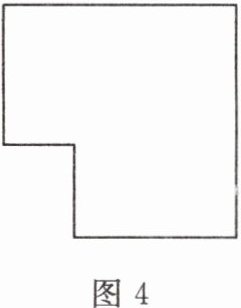
6. 现有如图4所示的一块均匀模板,请只用无刻度的直尺和铅笔画出它的重心.
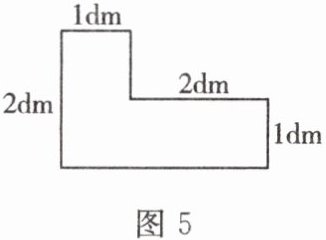
7. 如图5,请建立适当的平面直角坐标系,用坐标表示该图形的重心位置.
1. 取一块质地均匀的三角形木板,顶住三角形的某一个点,若这块木板能保持平衡,则这个点是( )
A. 三角形的一个顶点
B. 三角形的一条边的中点
C. 三角形三条中线的交点
D. 三角形三条高所在直线的交点
2. 如图1所示的网格由边长相同的小正方形组成,点A,B,C,D,E,F,G在小正方形的格点上,则$\triangle ABC$的重心是( )
A. 点D B. 点E C. 点F D. 点G


3. 如图2,乐乐用细线绑一块木板,然后提着细线使木板悬空. 乐乐发现,当将细线在A,C处捆绑木板时,木板不能水平悬空,而将细线在B处捆绑时,木板能水平悬空,则可以确定木板的重心在____处.
4. 通过查阅资料和使用悬挂法测定可知,线段的重心是____,正方形的重心是____,长方形的重心是____,平行四边形的重心是____,圆的重心是____.
活动二 确定平面组合图形的重心位置
5. 如图3,根据多边形ABCDEF在平面直角坐标系中的位置,可以确定这个多边形的重心坐标为____.
6. 现有如图4所示的一块均匀模板,请只用无刻度的直尺和铅笔画出它的重心.


7. 如图5,请建立适当的平面直角坐标系,用坐标表示该图形的重心位置.

答案:
1.C 2.A 3.B 4.线段的中点 对角线的交点 对角线的交点 对角线的交点 圆心 5.(1,0) 6.解:如图,把模板分成两个长方形,连接各自的重心;把模板重新分成两个长方形,得到连接各自重心的第二条线段,两条线段的交点G即为重心. 7.解:建立如图所示的平面直角坐标系.延长BC交x轴于点F.
7.解:建立如图所示的平面直角坐标系.延长BC交x轴于点F. 易得四边形ABFO的面积是2dm².其重心坐标是(0.5,1),四边形CDEF的面积是2dm²,其重心坐标是(2,0.5),所以该图形的重心坐标为$(\frac{2}{2+2}× 0.5+\frac{2}{2+2}× 2,\frac{2}{2+2}× 1+\frac{2}{2+2}× 0.5)$,即(1.25,0.75).
易得四边形ABFO的面积是2dm².其重心坐标是(0.5,1),四边形CDEF的面积是2dm²,其重心坐标是(2,0.5),所以该图形的重心坐标为$(\frac{2}{2+2}× 0.5+\frac{2}{2+2}× 2,\frac{2}{2+2}× 1+\frac{2}{2+2}× 0.5)$,即(1.25,0.75).
1.C 2.A 3.B 4.线段的中点 对角线的交点 对角线的交点 对角线的交点 圆心 5.(1,0) 6.解:如图,把模板分成两个长方形,连接各自的重心;把模板重新分成两个长方形,得到连接各自重心的第二条线段,两条线段的交点G即为重心.
 7.解:建立如图所示的平面直角坐标系.延长BC交x轴于点F.
7.解:建立如图所示的平面直角坐标系.延长BC交x轴于点F. 易得四边形ABFO的面积是2dm².其重心坐标是(0.5,1),四边形CDEF的面积是2dm²,其重心坐标是(2,0.5),所以该图形的重心坐标为$(\frac{2}{2+2}× 0.5+\frac{2}{2+2}× 2,\frac{2}{2+2}× 1+\frac{2}{2+2}× 0.5)$,即(1.25,0.75).
易得四边形ABFO的面积是2dm².其重心坐标是(0.5,1),四边形CDEF的面积是2dm²,其重心坐标是(2,0.5),所以该图形的重心坐标为$(\frac{2}{2+2}× 0.5+\frac{2}{2+2}× 2,\frac{2}{2+2}× 1+\frac{2}{2+2}× 0.5)$,即(1.25,0.75). 查看更多完整答案,请扫码查看


