《2025年三维数字课堂八年级数学上册人教版》

1.【空间观念】如图 1 所示,以 3 根等长的小棒为边,可以组成一个三角形,用 6 根等长的小棒为边最多可以组成几个等边三角形？9 根等长的小棒最多可以组成几个等边三角形？在平面内,用 6 根等长的小棒最多可以组成 2 个三角形,但在空间里却能组成 4 个等边三角形,因此本题要从空间去考虑.用 6 根等长的小棒能拼成边长为一根小棒长的 4 个等边三角形吗？用 9 根等长的小棒能拼成 7 个等边三角形吗？请你想一想,并画出图形.

答案：
能，画出图形如图所示.
　　　

2.【推理能力】从一个 $ n $ 边形的一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成 5 个三角形,则 $ n $ 的值是( )

A.6
B.7
C.8
D.9

答案： B

3. 从多边形的一个顶点出发可引出 6 条对角线,则它是( )

A.七边形
B.八边形
C.九边形
D.十边形

答案： C

4. 过 $ m $ 边形的一个顶点有 4 条对角线,$ n $ 边形没有对角线,$ k $ 边形共有 $ k $ 条对角线,则 $ (m - k)^n = $____.

答案： 8　点拨:m=7,n=3,k=5.

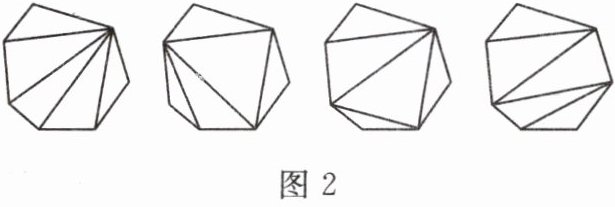
5. 已知：把一个多边形用连接它的不相邻顶点的线段(这些线段不在多边形内部相交)划分为若干个三角形,叫作多边形的三角剖分. 如图 2 所示的是七边形的三角剖分的几种方法.

(1) 请画出六边形的一种三角剖分方法,并指出能剖分出多少个三角形？$ m $ 边形呢？
(2) 对于一个 $ m $ 边形的一种三角剖分,若这些三角形的内角总和是 $ 2700^{\circ} $,求 $ m $ 的值.
(3) 一个多边形,往往有多种方法进行三角剖分. 记 $ m $ 边形三角剖分的方法数为 $ D_m $,则当 $ m \geq 3 $ 时,$ \frac{D_{m + 1}}{D_m} = \frac{4m - 6}{m} $. 已知 $ D_3 = 1 $,求八边形的三角剖分方法数 $ D_8 $.

答案：
5.解:
(1)如图所示(答案不唯一)，能剖分出4个三角形.m边形可三角剖分为(m−2)个三角形.
　　　　　　　
(2)由
(1)可知,m边形可三角剖分为(m−2)个三角形，这些三角形的内角总和为(m-2)×180°,
∴(m−2)×180°=2700°,解得m=17.
(3)将m=3代入$\frac {D_{m+1}}{D_{m}}=\frac {4m-6}{m}$，得$\frac {D_{4}}{D_{3}}=\frac {4×3-6}{3}=\frac {12-6}{3}=\frac {6}{3}=2.$
∵D₃=1,
∴D₄=2D₃=2×1=2.
　将m=4代入$\frac {D_{m+1}}{D_{m}}=\frac {4m-6}{m}$，得$\frac {D_{5}}{D_{4}}=\frac {4×4-6}{4}=\frac {16-6}{4}=\frac {10}{4}=\frac {5}{2}.$
∵D₄=2,
∴D₅=$\frac {5}{2}$D₄=$\frac {5}{2}$×2=5.
　以此类推D₈=132.
∴八边形的三角剖分方法数D₈=132.