《2025年三维数字课堂八年级数学上册人教版》

3. 在做物理实验时,一位同学研究一个小木块在斜坡上滑下时的运动状态。如图 13 - 5,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 15^{\circ}$,三角形小木块$DEF在斜坡AB$上,且$DE // BC$,$EF // AC$,则$\angle DFE$的度数是( )

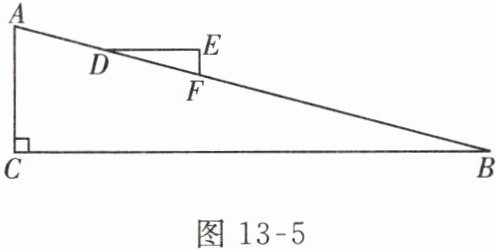
A.$15^{\circ}$
B.$65^{\circ}$
C.$75^{\circ}$
D.$85^{\circ}$

答案： C

4. 如图 13 - 6,将一副三角板的直角顶点重合并部分重叠。若$\angle BOD = 20^{\circ}$,则$\angle AEC$的度数为( )

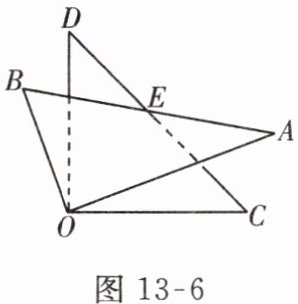
A.$30^{\circ}$


B.$35^{\circ}$
C.$40^{\circ}$
D.$45^{\circ}$

答案： B

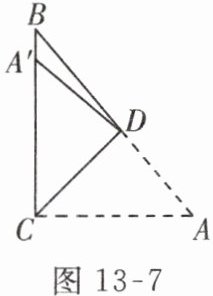
5. 如图 13 - 7,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 50^{\circ}$,将其折叠,使点$A落在边CB上的点A'$处,折痕为$CD$,则$\angle A'DB$的度数为( )

A.$40^{\circ}$
B.$30^{\circ}$
C.$20^{\circ}$
D.$10^{\circ}$

答案： D 点拨:
∵∠B=90°-∠A=40°,∠CA'D=∠A=50°,
∴∠A'DB=∠CA'D-∠B=50°-40°=10°.

6. 小颖一笔画成了如图 13 - 8 所示的图形,若$\angle A = 60^{\circ}$,则$\angle B + \angle C + \angle D + \angle E = $( )

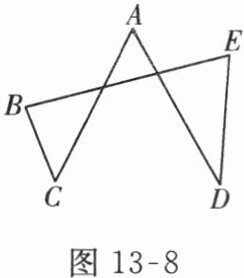
A.$180^{\circ}$


B.$240^{\circ}$
C.$270^{\circ}$
D.$300^{\circ}$

答案： B

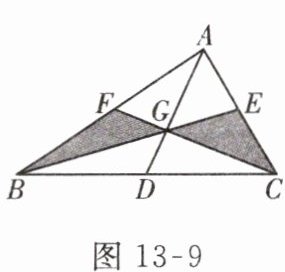
7. 如图 13 - 9,$G为\triangle ABC三边中线AD$,$BE$,$CF$的交点,$S_{\triangle ABC} = 12cm^{2}$,则阴影部分的面积为( )

A.$4cm^{2}$
B.$5cm^{2}$
C.$6cm^{2}$
D.$8cm^{2}$

答案： A

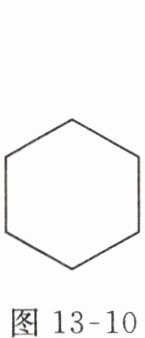
8. 如图 13 - 10,六根木条钉成一个六边形框架,要使框架稳固且不活动,至少还需要添加______根木条。

答案： 3

9. 如果一个等腰三角形的两边长分别为$4cm和6cm$,那么这个三角形的周长是______。

答案： 14cm 或 16cm 点拨:4cm 和 6cm 长的线段哪一个可以作为腰,应利用三角形中“两边之和大于第三边”进行讨论:①若腰长是4cm,较小两边之和为4+4=8(cm),则4+4＞6,这时可以组成等腰三角形;②若腰长是6cm,较小两边之和为6+4=10(cm),则6+4＞6,也可以组成等腰三角形.由①②可知在这两种情况下都可以组成三角形.

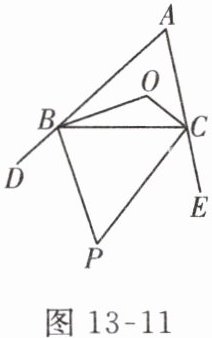
10. 如图 13 - 11,$\triangle ABC的两条内角平分线BO$,$CO相交于点O$,两条外角平分线$BP$,$CP相交于点P$。已知$\angle BOC = 120^{\circ}$,则$\angle P = $______。

答案： 60°

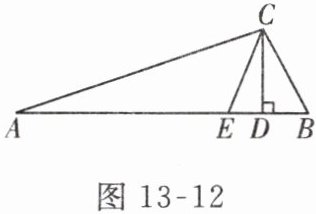
11. 如图 13 - 12,在$\triangle ABC$中,$CD \perp AB于点D$,$CE是\angle ACB$的平分线,$\angle A = 20^{\circ}$,$\angle B = 60^{\circ}$。求$\angle BCD和\angle ECD$的度数。

答案： 解:
∵CD⊥AB,
∴∠CDB=∠CDE=90°.
∵∠B=60°,
∴∠BCD=90°-∠B=90°-60°=30°.
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°.
∵CE是∠ACB的平分线,
∴∠ACE=1/2∠ACB=50°.
∴∠CEB=∠A+∠ACE=20°+50°=70°.
∴∠ECD=90°-70°=20°.