《2025年三维数字课堂八年级数学上册人教版》

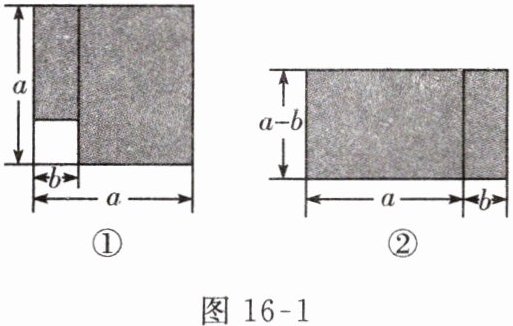
【例 1】如图 16 - 1 所示,将两个长方形用不同方式拼成图 16 - 1①和图 16 - 1②两个图形。
(1)若图①中的阴影部分面积为$a^{2}-b^{2}$,则图②中的阴影部分面积为______(用含字母$a$,$b$的代数式表示)。
(2)由(1)你可以得到的等式是______。
(3)根据你所得到的等式解决下面的问题：
①若$x^{2}-y^{2}= 16$,$x - y = 2$,则$x + y = $______；
②计算：$67.75^{2}-32.25^{2}$。

思路分析：通过对条件的转化、结论的转化,使问题化难为易,化生为熟,化未知为已知,最终解决问题,这个过程体现了转化的思想方法。
解：(1)$(a + b)(a - b)$
(2)$a^{2}-b^{2}= (a + b)(a - b)$
(3)①$8$
②原式$=(67.75 + 32.25)×(67.75 - 32.25)= 100×35.5 = 3550$。

答案：
(1) $ (a - b)(a + b) $ 或 $ (a + b)(a - b) $
(2) $ a^2 - b^2 = (a + b)(a - b) $
(3) ① $ x + y = 8 $
② $ 67.75^2 - 32.25^2 = (67.75 + 32.25) × (67.75 - 32.25) = 100 × 35.5 = 3550 $

【例 2】已知多项式$A= (m - 3)^{2}-(2 - m)(2 + m)+2$。
(1)化简多项式$A$；
(2)若$x^{2}-2mx + 4$是一个完全平方式,求$A$的值。
思路分析：当不能确定完全平方公式的类型时往往需要进行分类讨论。
解：(1)$A= (m - 3)^{2}-(2 - m)(2 + m)+2= m^{2}-6m + 9-(4 - m^{2})+2= m^{2}-6m + 9 - 4 + m^{2}+2 = 2m^{2}-6m + 7$。
(2)$\because x^{2}-2mx + 4$是一个完全平方式,$\therefore -2m= \pm2×1×2$,$\therefore m= \pm2$。当$m = 2$时,$A = 2×2^{2}-6×2 + 7 = 8 - 12 + 7 = 3$；当$m = - 2$时,$A = 2×(-2)^{2}-6×(-2)+7 = 8 + 12 + 7 = 27$。故$A的值为3或27$。

答案：
(1) $A=(m - 3)^{2}-(2 - m)(2 + m)+2$
$=m^{2}-6m + 9-(4 - m^{2})+2$
$=m^{2}-6m + 9 - 4 + m^{2}+2$
$=2m^{2}-6m + 7$。
(2) $\because x^{2}-2mx + 4$是一个完全平方式，
$\therefore -2m=\pm 2×1×2$，
$\therefore m=\pm 2$。
当$m=2$时，$A=2×2^{2}-6×2 + 7=8 - 12 + 7=3$；
当$m=-2$时，$A=2×(-2)^{2}-6×(-2)+7=8 + 12 + 7=27$。
故$A$的值为$3$或$27$。

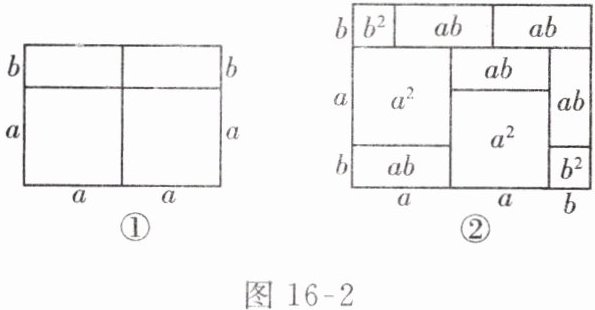
【例 3】阅读材料并解答问题：我们已经知道,完全平方公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如：$2a(a + b)= 2a^{2}+2ab$就可以用如图 16 - 2①所示的图形面积来表示。
(1)请写出图 16 - 2②所表示的代数恒等式。
(2)请画图,用平面几何图形的面积来表示代数恒等式$(a + b)(2a + b)= 2a^{2}+3ab + b^{2}$。

思路分析：数形结合是指“以形助数”或“以数解形”,即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的。
解：(1)$(2a + b)(a + 2b)= 2a^{2}+5ab + 2b^{2}$。
(2)如图 16 - 3 所示即为所求。

答案：
(1)$(2a + b)(a + 2b)=2a^2 + 5ab + 2b^2$
(2)（在答题卡上画出长为$2a + b$、宽为$a + b$的长方形，内部划分如下：横向分为$a$、$a$、$b$，纵向分为$a$、$b$；其中，纵向$a$与横向$a$构成的两个小长方形面积为$a^2$，纵向$a$与横向$b$构成的小长方形面积为$ab$，纵向$b$与横向$a$构成的两个小长方形面积为$ab$，纵向$b$与横向$b$构成的小正方形面积为$b^2$，图形略）