《2025年三维数字课堂八年级数学上册人教版》

1. 【分类讨论思想】在 $ Rt \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ \angle A = 30^{\circ} $,$ AB = 8 $.若点 $ D $ 在直线 $ AB $ 上(不与点 $ A $,$ B $ 重合),且 $ \angle BCD = 30^{\circ} $,则 $ AD $ 的长为______.

答案： 6或12

2. 如图 15 - 3 - 53,在平面直角坐标系 $ xOy $ 中,$ Rt \triangle OAB $ 的斜边 $ OB $ 在 $ x $ 轴上,$ \angle ABO = 30^{\circ} $,若点 $ A $ 的横坐标为 $ 1 $,则点 $ B $ 的坐标为______.

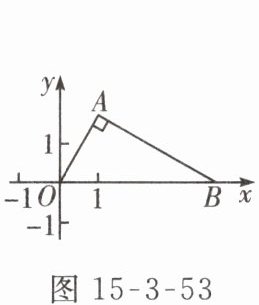
答案： (4,0)

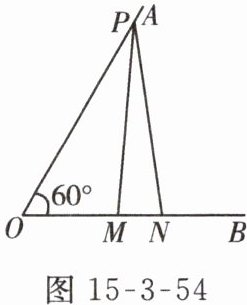
3. 如图 15 - 3 - 54,$ \angle AOB = 60^{\circ} $,点 $ P $ 在边 $ OA $ 上,$ OP = 12 $,点 $ M $,$ N $ 在边 $ OB $ 上,$ PM = PN $.若 $ MN = 2 $,则 $ OM = $______.

答案： 5

4. 【实际应用】如图 15 - 3 - 55,某轮船由西向东航行,在 $ A $ 处测得小岛 $ P $ 的方位是北偏东 $ 75^{\circ} $,又继续航行 $ 7 $ 海里后,在 $ B $ 处测得小岛 $ P $ 的方位是北偏东 $ 60^{\circ} $.
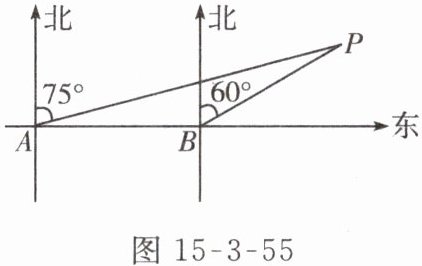
(1)此时轮船与小岛 $ P $ 的距离 $ BP $ 是多少海里？
(2)小岛 $ P $ 方圆 $ 3 $ 海里内有暗礁,如果轮船继续向东航行,请问轮船有没有触礁的危险？请说明理由.

答案： 解:
(1)过点P作PD⊥AB于点D.
∵∠PBD=90°−60°=30°,
　且∠PBD=∠PAB+∠APB,∠PAB=90°−75°=15°,
∴∠APB=15°,
∴∠PAB=∠APB,
∴BP=AB=7海里.
(2)轮船没有触礁的危险.理由:
　由
(1),得在Rt△PBD中,BP=7海里，∠PBD=30°,∠PDB=90°,
∴PD=$\frac{1}{2}$PB=3.5海里.
∵3.5＞3,
∴该轮船继续向东航行没有触礁的危险.

5. 如图 15 - 3 - 56,在 $ \triangle ABC $ 中,$ AB = AC $,$ \angle BAC = 120^{\circ} $,$ AC $ 的垂直平分线 $ EF $ 交 $ AC $ 于点 $ E $,交 $ BC $ 于点 $ F $.求证 $ BF = 2CF $.

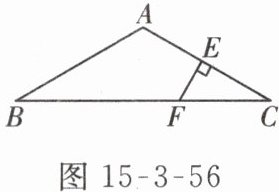
答案： 证明:连接AF.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=$\frac{180° - 120°}{2}$=30°.
　又
∵EF是AC的垂直平分线，
∴AF=CF,
∴∠C=∠FAC=30°,
∴∠BAF=∠BAC−∠FAC=120°−30°=90°.
　在Rt△BAF中,∠BAF=90°,∠B=30°,
∴AF=$\frac{1}{2}$BF,
∴CF=$\frac{1}{2}$BF,即BF=2CF.

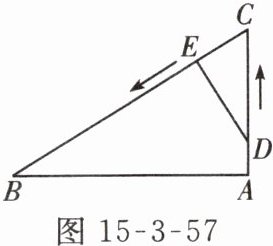
如图 15 - 3 - 57,在 $ \triangle ABC $ 中,$ \angle A = 90^{\circ} $,$ \angle B = 30^{\circ} $,$ AC = 3cm $,点 $ D $ 以 $ 1cm/s $ 的速度从点 $ A $ 向点 $ C $ 运动,同时点 $ E $ 以 $ 2cm/s $ 的速度从点 $ C $ 向点 $ B $ 运动,运动时间为 $ ts $.
(1)当 $ t = $______时,$ \triangle DEC $ 为等边三角形.
(2)当 $ t $ 为何值时,$ \triangle DEC $ 为直角三角形？

答案：
(1)1
(2)解:在△ABC中,
∵∠A=90°,∠B=30°,
∴∠C=90°−30°=60°.
由题意,得AD=tcm,CE=2tcm,
∴CD=(3−t)cm.
①当∠DEC为直角时,∠EDC=30°.
∴CE=$\frac{1}{2}$CD,即2t=$\frac{1}{2}$(3−t),解得t=$\frac{3}{5}$;
②当∠EDC为直角时,∠DEC=30°,
∴CD=$\frac{1}{2}$CE,即3−t=$\frac{1}{2}$×2t,解得t=$\frac{3}{2}$.
综上所述，当t=$\frac{3}{5}$或t=$\frac{3}{2}$时，△DEC为直角三角形.