第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
1. 如图14-2-38,以$\triangle ABC的顶点A$为圆心,以$BC$长为半径作弧;再以顶点$C$为圆心,以$AB$长为半径作弧,两弧交于点$D$;连接$AD$,$CD$。由作法可得$\triangle ABC \cong \triangle CDA$的根据是 ( )

A.SAS
B.ASA
C.AAS
D.SSS
]

A.SAS
B.ASA
C.AAS
D.SSS
]
答案:
D
2. 如图14-2-39①,已知$\angle \alpha$,$\angle \beta$,线段$m$,求作$\triangle ABC$,使$\angle A = \angle \alpha$,$\angle B = \angle \beta$,$AB = m$。
① ②

作法:如图14-2-39②,作线段$AB = m$;在$AB的同旁作\angle A = \angle \alpha$,$\angle B = \angle \beta$,$\angle A与\angle B的另一边交于点C$,则$\triangle ABC$就是所求作的三角形。这样作图的依据是( )
A.SAS
B.SSS
C.ASA
D.AAS
① ②

作法:如图14-2-39②,作线段$AB = m$;在$AB的同旁作\angle A = \angle \alpha$,$\angle B = \angle \beta$,$\angle A与\angle B的另一边交于点C$,则$\triangle ABC$就是所求作的三角形。这样作图的依据是( )
A.SAS
B.SSS
C.ASA
D.AAS
答案:
C
3. 下列尺规作图中,不一定能判定直线$a平行于直线b$的是( )
A B
C D

A B
C D

答案:
C
4. 如图14-2-40,在$\triangle ABC$中,$O是边AB$上的点。按下列要求作图:
①以点$B$为圆心,适当长为半径画弧,交线段$BO于点D$,交线段$BC于点E$;
②以点$O$为圆心,$BD$长为半径画弧,交线段$OA于点F$;
③以点$F$为圆心,$DE$长为半径画弧,交前一条弧于点$G$,点$G与点C在直线AB$的同侧;
④作直线$OG$,交线段$AC于点M$。
下列结论不一定成立的是 ( )
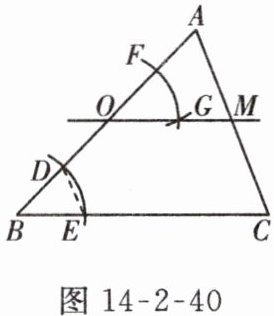
A.$\angle AOM = \angle B$
B.$\angle OMC + \angle C = 180^{\circ}$
C.$OM // BC$
D.$\angle B = \angle AMO$
]
①以点$B$为圆心,适当长为半径画弧,交线段$BO于点D$,交线段$BC于点E$;
②以点$O$为圆心,$BD$长为半径画弧,交线段$OA于点F$;
③以点$F$为圆心,$DE$长为半径画弧,交前一条弧于点$G$,点$G与点C在直线AB$的同侧;
④作直线$OG$,交线段$AC于点M$。
下列结论不一定成立的是 ( )

A.$\angle AOM = \angle B$
B.$\angle OMC + \angle C = 180^{\circ}$
C.$OM // BC$
D.$\angle B = \angle AMO$
]
答案:
D 点拨:由作图,可知∠AOM=∠B,
∴OM//BC,
∴∠OMC+∠C=180°,故选项A,B,C正确.故选D.
∴OM//BC,
∴∠OMC+∠C=180°,故选项A,B,C正确.故选D.
5. 如图14-2-41,已知$\triangle DEF$,线段$AB$,$AB = DE$,用尺规以$AB为一条边作出\triangle ABC$,使其与$\triangle DEF$全等,这样的三角形能作____个。


答案:
4
6.【教材P40例5变式】如图14-2-42,已知线段$a$,$b和\angle \alpha$,求作$\triangle ABC$,使得$AB = 2a$,$AC = b$,$\angle BAC = \angle \alpha$。(不写作法,保留作图痕迹)
]

]

答案:
解:如图所示,△ABC即为所求作的三角形.
解:如图所示,△ABC即为所求作的三角形.

查看更多完整答案,请扫码查看


