《2025年三维数字课堂八年级数学上册人教版》

1. 如图 1,图中所有小三角形均是全等的等边三角形,其中的四边形 $ AEFG $ 可以看成把四边形 $ ABCD $ 以点 $ A $ 为旋转中心( )

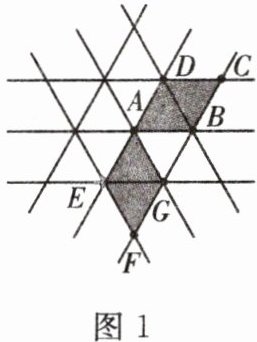
A.顺时针旋转 $ 60^{\circ} $ 得到的
B.顺时针旋转 $ 120^{\circ} $ 得到的
C.逆时针旋转 $ 60^{\circ} $ 得到的
D.逆时针旋转 $ 120^{\circ} $ 得到的

答案： B

2. 【一题多法】如图 2,是一个正方形的门窗,在装修房屋时,为了把它设计成美观大方的图案,要求在正方形中设计若干个全等的三角形,使其面积和等于正方形的面积. 请你按要求在正方形中画出你设计的图形.

答案：
解:本题属开放性题目,答案不唯一.如图
(1)
(2)
(3)所示是根据全等三角形的性质设计的图形,同学们可自己另外设计一些其他的图形.

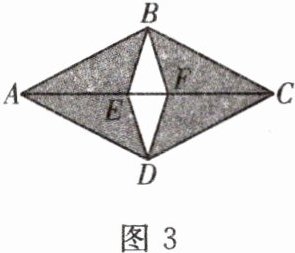
3. 如图 3 是某房间地砖的一个图案,其中 $ AB = BC = CD = DA $,$ BE = DE = DF = FB $,图案由有花纹的全等三角形木块(阴影部分)和无花纹的全等三角形木块(中间部分)拼成,这个图案的面积是 $ 0.05m^{2} $,若房间的面积是 $ 23m^{2} $,则最少需要有花纹的三角形木块和无花纹的木块各多少块？

答案： 解:铺设整个房间需要像四边形 ABCD 这样的图案的块数为23÷0.05=460(块),而四边形 ABCD 是由4块有花纹的和2块无花纹的三角形木块组成,故需要有花纹的木块的数量为460×4=1840(块),需要无花纹的木块的数量为460×2=920(块).

4. 如图 4,某建筑模型有两层型滑梯,每层的高度相同($ EH = HD $),都为 2 米,小明想知道左右两个滑梯 $ BC $ 和 $ EF $ 的长度是否相等,于是制定了如下方案：
|课题|探究两个滑梯的长度是否相等|
|测量工具|长度为 5 米的米尺|
|测量步骤|①测量出线段 $ FD $ 的长度；②测量出线段 $ AB $ 的长度|
|测量数据| $ DF = 2 $ 米,$ AB = 4 $ 米|

(1) 根据小明的测量方案和数据,判断两个滑梯 $ BC $ 和 $ EF $ 的长度是否相等,并说明理由.
(2) 试猜想左右两个滑梯 $ BC $ 和 $ EF $ 所在直线的位置关系并加以证明.

答案：
解:
(1)BC=EF.理由如下:由题意,可知∠CAB=∠EDF=90°,DF=DH=AC=2米,DE=2×2=4(米).
∴DE=AB.在△ABC和△DEF中,$\left\{\begin{array}{l} AB=DE,\\ ∠CAB=∠FDE,\\ AC=DF,\end{array}\right. $
∴△ABC≌△DEF(SAS).
∴BC=EF.
(2)BC⊥EF.证明:延长 BC 交 EF 于点 G.
∵△ABC≌△DEF,
∴∠BCA=∠EFD.
∵∠BAC=90°,
∴∠CBA+∠BCA=90°.
∴∠CBA+∠EFD=90°.
∴∠BGF=180°-(∠CBA+∠EFD)=90°.
∴BC⊥EF.