《2025年三维数字课堂八年级数学上册人教版》

1. 下列说法：①线段的对称轴有两条；②角是轴对称图形,它的平分线就是它的对称轴；③两点关于连接它们的线段的垂直平分线对称；④到直线$l的距离相等的两个点关于直线l$对称. 其中正确的有( )

A.4 个
B.3 个
C.2 个
D.1 个

答案： C

2. 如图 15-1-7,在四边形$ABCD$中,对角线$BD$所在的直线是其对称轴,点$E是直线BD$上的点,已知$\triangle ABE$的周长为 15,$AE = 5$,$BE = 4$,则$EC$,$BC$的长分别为( )


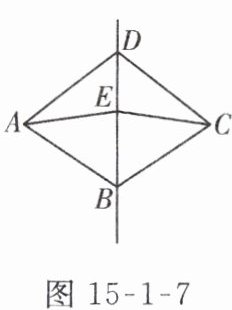
A.4,5
B.4,6
C.5,6
D.5,5

答案： C

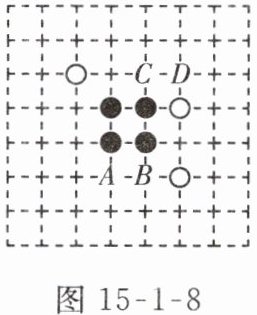
3.【传统文化】围棋起源于中国,古代称为“弈”.
如图 15-1-8 是两位同学的部分对弈图,轮到白方落子,观察棋盘,白方若落子于点______的位置,则所得的对弈图是轴对称图形.(填写$A$,$B$,$C$,$D$中的一处即可,$A$,$B$,$C$,$D$位于棋盘的格点上)

答案： A(或C)

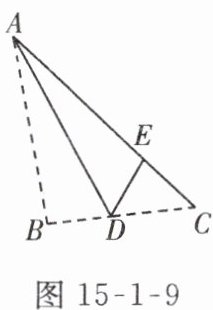
4. 如图 15-1-9,在$\triangle ABC$中,$AB = 6$,$BC = 5$,将$\triangle ABD沿AD$折叠,使点$B恰好落在AC边上的点E$处,若$\triangle DEC$的周长为 7,则$AC$的长为______.

答案： 8 点拨:
∵将△ABD沿AD折叠,使点B恰好落在AC边上的点E处,
∴BD=DE,AB=AE.
∵△DEC的周长为7,
∴DE+CE+CD=BD+CE+CD=BC+CE=7,
∴CE=7-BC=2,
∴AC=AE+CE=AB+CE=6+2=8.

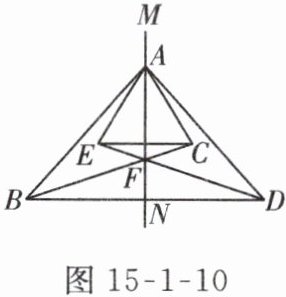
5. 如图 15-1-10,$\triangle ABC和\triangle ADE关于直线MN$对称,$BC和DE的交点F在直线MN$上.
(1) 图中点$B$的对应点是点______,$\angle AED$的对应角是______；
(2) 若$ED = 9$,$BF = 6$,求$EF$的长；
(3) 连接$BD和EC$,判断$BD和EC$的位置关系,并说明理由.

答案：
(1)D ∠ACB；
(2)由题,易得DF=BF=6,
∵ED=9,
∴EF=ED-DF=9-6=3；
(3)平行.理由如下:
∵△ABC和△ADE关于直线MN对称,
∴MN⊥EC,MN⊥BD,
∴EC//BD.

如图 15-1-11,点$P在\angle AOB$的内部,点$C和点P关于OA$对称,点$P和点D关于OB$对称,连接$CD交OA于点M$,交$OB于点N$,连接$PM$,$PN$.
(1)①若$\angle AOB = 60^{\circ}$,求$\angle COD$的度数.
②若$\angle AOB = n^{\circ}$,则$\angle COD = $______(用含$n$的代数式表示).
(2)若$CD = 4$,则$\triangle PMN$的周长为______.

答案：
(1)①解:
∵点C和点P关于OA对称,点M在直线OA上,
∴△COM与△POM关于直线OA对称.
∴∠AOC=∠AOP.同理,可得∠BOD=∠BOP.
∴∠COD=∠AOC+∠AOP+∠BOP+∠BOD=2(∠AOP+∠BOP)=2∠AOB=2×60°=120°.②2n°；
(2)4 点拨:由点C和点P关于OA对称,点P和点D关于OB对称,得PM=MC,PN=ND,
∴PM+MN+PN=CD=4.