《2025年三维数字课堂八年级数学上册人教版》

1. 【实际应用】为方便劳动技术小组实践教学,需用篱笆围一块三角形空地,现已连接好三段篱笆 AB,BC,CD,这三段篱笆的长度如图 13-2-4 所示,其中篱笆 AB,CD 可分别绕轴 BE 和 CF 转动. 若要围成一个三角形的空地,则在篱笆 CD 上接上新的篱笆的长度可以为( )

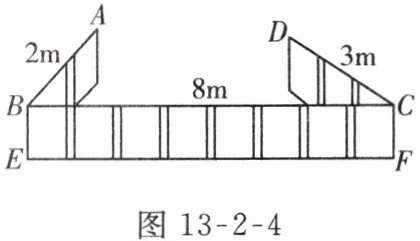
A.1m
B.2m
C.3m
D.4m
]

答案： D

2. 若 a,b,c 为△ABC 的三边长,且满足|a-4|+(b-2)2= 0,则 c 的值可以为( )

A.5
B.6
C.7
D.8

答案： A　点拨:
∵|a - 4|+(b - 2)² = 0,
∴a = 4,b = 2,
∴2＜c＜6,故选A.

3. 如图 13-2-5,为使由五根木棒组成的架子不变形,至少还要在架子上钉上的木棒根数是( )

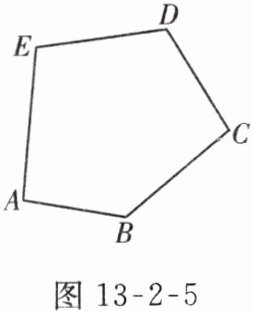
A.0
B.1
C.2
D.5
]

答案： C

4. 【阅读理解】在一个三角形中,如果有一条边的长是另一条边的长的 2 倍,且有两条边的和是另一条边的 2 倍,那么我们就把这样的三角形叫 2 倍边三角形. 如果一个 2 倍边三角形中有一条边长为 6,则这个三角形的另外两条边的和可以是______.

答案： 21或7.5或12　点拨:设最短边为x，其他两边分别为2x,1.5x，当x = 6时，其他两边为12,9,因为6 + 9＞12,符合题意，12 + 9 = 21;当2x = 6时,其他两边为3,4.5,因为3 + 4.5＞6,符合题意,3 + 4.5 = 7.5;当1.5x = 6时，其他两边为4,8,因为4 + 6＞8,符合题意,4 + 8 = 12,故答案为21或7.5 或12.

5. 用一条长为 20cm 的细绳围成一个等腰三角形.
(1)如果腰长是底边长的 2 倍,那么各边的长分别是多少?
(2)能围成有一边长为 5cm 的等腰三角形吗?如果能,请求出它的另两边的长.

答案： 解:
(1)设底边长为xcm，则腰长为2xcm.依题意，得
　2x + 2x + x = 20,解得x = 4.
∴2x = 8.
∴各边的长分别为8cm，8cm,4cm.
(2)①当底边长为5cm时，腰长为(20 - 5)÷2 = 7.5(cm),能构成三角形;
　②当腰长为5cm时，底边长为20 - 2×5 = 10(cm),
∵5 + 5 = 10,
∴不能构成三角形，故舍去.
∴能围成有一边长为5cm的等腰三角形，另两边的长分别为7.5cm,7.5cm.

观察并探求下列各问题：

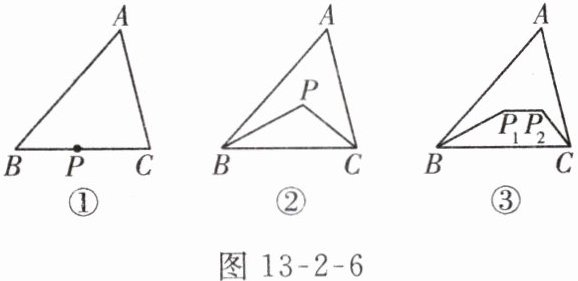
(1)如图 13-2-6①,在△ABC 中,P 为边 BC 上一点,则 BP+PC______AB+AC(填“＞”“＜”或“=”).
(2)如图 13-2-6②,将(1)中的点 P 移到△ABC 内,试观察比较,△BPC 的周长______△ABC 的周长(填“＞”“＜”或“=”).
(3)如图 13-2-6③,将(2)中的点 P 变为两个点 P1,P2,试观察比较四边形 BP1P2C 的周长与△ABC 的周长的大小.

答案：
解:
(1)＜
(2)＜　点拨:如图，延长BP交AC于点M，在△ABM中，
BP + PM＜AB + AM,①
在△PMC中,PC＜PM + MC,②
① + ②,得BP + PC＜AB + AC,
∴△BPC的周长＜△ABC的周长.

(3)如图，分别延长BP₁，CP₂交于点M,
由
(2)知BM + CM＜AB + AC,
又
∵P₁P₂＜P₁M + P₂M,
∴BP₁ + P₁P₂ + P₂C＜BM + CM＜AB + AC,
∴四边形BP₁P₂C的周长＜△ABC的周长.