《2025年三维数字课堂八年级数学上册人教版》

1. 点 $ A,B $ 关于直线 $ a $ 对称,$ P $ 是直线 $ a $ 上任意一点,下列说法不正确的是( )

A.直线 $ AB $ 是直线 $ a $ 的垂线
B.直线 $ a $ 是点 $ A $ 和点 $ B $ 的对称轴
C.线段 $ PA $ 与线段 $ PB $ 相等
D.若 $ PA = PB $,则 $ P $ 是 $ AB $ 的中点

答案： D

2. 如图 15 - 2 - 1,已知直线 $ l $ 和 $ \triangle DEF $,画出 $ \triangle DEF $ 关于直线 $ l $ 对称的图形. 将作图步骤补充完整：

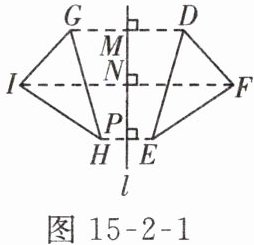
(1) 分别过点 $ D,E,F $ 作直线 $ l $ 的垂线,垂足分别是______；
(2) 在垂线上分别取点______,使______ $ = DM $,______ $ = EP $,______ $ = FN $；
(3) 连接______,______,______,则 $ \triangle GHI $ 即为所求.

答案：
(1)M,P,N　
(2)G,H,I　GM　HP　IN
(3)GH　GI　HI

3. 在纸条上写上汉字“日、出、西、山”四个字,并将纸条竖直且垂直于挂在墙上的镜子摆放,则这四个字中,在镜子中的像与原字一样的字有______.

答案： 日、出、山

4. 【教材 $ P73 $ 练习 $ 1 $ 变式】如图 15 - 2 - 2,画出下列 $ \triangle ABC $ 关于直线 $ l $ 对称的图形.

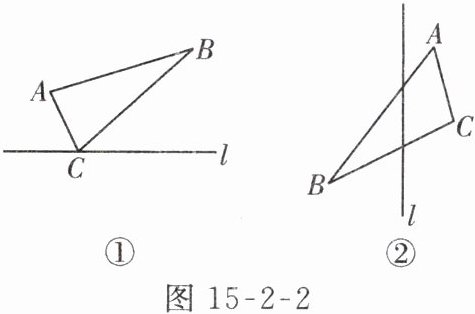
答案：
解:如图①②.
　　　　 　　

1. 下列各图为小华在镜中看到身后墙上的钟,你认为实际时间最接近 $ 8 $ 时的是( )
A.
B.
C.
D.

答案： D

2. 【抽象能力】在如图 15 - 2 - 3 所示的 $ 3×3 $ 的网格图中,再在其中一个小方格中画上半径相等的圆,使三个圆为轴对称图形,方法有( )

A.$ 2 $ 种
B.$ 3 $ 种
C.$ 4 $ 种
D.$ 5 $ 种

答案： D

3. 如图 15 - 2 - 4,在小等边三角形组成的网格中,已有 $ 6 $ 个小等边三角形被涂色,还需再涂 $ 2 $ 个小等边三角形,使它们与原来涂色的小等边三角形组成的新图案恰好为轴对称图形,则填涂的方案有( )

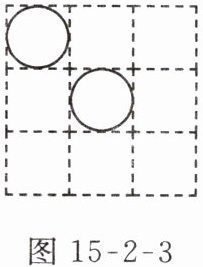
A.$ 3 $ 种
B.$ 4 $ 种
C.$ 5 $ 种
D.$ 6 $ 种

答案：
3.D　点拨:如图,共有6种填涂方案.故选D.
　　　

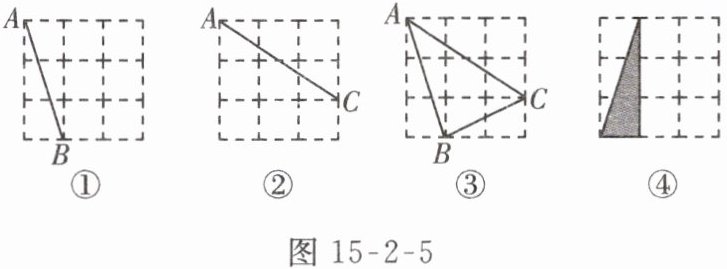
4. 图 15 - 2 - 5①、②、③、④都是 $ 3×3 $ 的正方形网格,每个小正方形的顶点称为格点. $ A,B,C $ 均为格点,在给定的网格中,按下列要求画图.
(1) 在图 15 - 2 - 5①中,画一条不与 $ AB $ 重合的线段 $ MN $,使 $ MN $ 与 $ AB $ 关于某条直线对称,且 $ M,N $ 为格点；
(2) 在图 15 - 2 - 5②中,画一条不与 $ AC $ 重合的线段 $ PQ $,使 $ PQ $ 与 $ AC $ 关于某条直线对称,且 $ P,Q $ 为格点；
(3) 在图 15 - 2 - 5③中,画一个 $ \triangle DEF $,使 $ \triangle DEF $ 与 $ \triangle ABC $ 关于某条直线对称,且 $ D,E,F $ 为格点；
(4) 画出 $ 3 $ 个与图 15 - 2 - 5④中的格点三角形成轴对称的三角形.

答案：
4.解:
(1)如图①,MN即为所求.(答案不唯一)
(2)如图②,PQ即为所求.(答案不唯一)
(3)如图③,△DEF即为所求.(答案不唯一)
　　　
(4)如图④.(答案不唯一)