《2025年一本预备新初一小升初数学》

3. 某艘轮船在河流中航行于A,B两码头之间,顺流航行全程需7h,逆流航行全程需9h.已知水流速度为每小时3km,求A,B两码头间的距离.若设A,B两码头间的距离为x km,则所列方程为(B)
A.$\frac{x}{7}+3= \frac{x}{9}-3$
B.$\frac{x}{7}-3= \frac{x}{9}+3$
C.$\frac{x}{7}+3= \frac{x}{9}$
D.$\frac{x}{7}-3= \frac{x}{9}$

答案： 设A,B两码头间的距离为x km。
顺流速度为$\frac{x}{7}$ km/h，逆流速度为$\frac{x}{9}$ km/h。
因为顺流速度=静水速度+水流速度，逆流速度=静水速度-水流速度，所以静水速度=顺流速度-水流速度=逆流速度+水流速度。
则$\frac{x}{7}-3=\frac{x}{9}+3$。
答案：B

4. 甲、乙两地间运行的火车提速后,速度比原来提高了45 km/h,结果两地之间的行车时间由原来的6h缩短了2h,则火车原来的速度是90km/h.

答案： 设火车原来的速度为 $x$ km/h。
根据题意，火车提速后的速度为 $x + 45$ km/h。
原来的行车时间为6h，所以原来的行驶距离为 $6x$ km。
提速后的行车时间为 $6 - 2 = 4$ h，所以提速后的行驶距离为 $4(x + 45)$ km。
由于两地之间的距离不变，所以我们可以得到方程：
$6x = 4(x + 45)$
展开并整理得：
$6x = 4x + 180$
$2x = 180$
$x = 90$
所以，火车原来的速度是 90 km/h。
答案：90 km/h。

5. 某件商品的进价是270元,打八折销售可获利润50元,则原售价为400元.

答案： 设商品的原始售价为$x$元。
根据题意，商品打八折销售，即售价为$0.8x$元，利润为$50$元，进价为$270$元。
因此，我们可以建立方程：
$0.8x - 270 = 50$
解这个方程，我们得到：
$0.8x = 320$
$x = \frac{320}{0.8}$
$x = 400$
答案：$400$元。

6. 某超市购进了一批书包,按成本价提高50%后标价销售,为了增加销量,又以九折优惠进行销售,每个书包的售价为108元.
(1)每个书包的成本价为多少元？请你用方程解此应用题.
(2)若这批书包一共购进100个,全部以108元的售价卖出,则该超市共盈利多少元？

答案： 6.解:
(1)每个书包的成本价为多少元？请你用方程解此应用题.设每个书包的成本价为x元,则标价为(1+50%)x元,九折优惠后售价为90%×(1+50%)x元.由题意,得90%×(1+50%)x=108,解得x=80.答:每个书包的成本价为80元.
(2)若这批书包一共购进100个,全部以108元的售价卖出,则该超市共盈利多少元？100×(108-80)=2800(元).答:该超市共盈利2800元.

7. A,B两地相距450 km,甲、乙两车分别从A,B两地同时出发,相向而行,已知甲车的速度为120 km/h,乙车的速度为80 km/h,经过t h两车相距50 km,则t的值是(D)
A.2
B.12.5
C.10或12.5
D.2或2.5

答案： D [解析]①当两车相遇之前相距50 km时,根据题意,得120t+80t+50=450,解得t=2;②当两车相遇之后相距50 km时,根据题意,得120t+80t-50=450,解得t=2.5.综上,t的值是2或2.5.

8. 国庆期间,某超市进行换季打折活动.小明以八折的优惠购买了一件运动服,节省了16元,那么他购买这件衣服实际用了64元.

答案： 64 [解析]设这件衣服的原价为x元.由题意,得(1-80%)x=16,解得x=80.80-16=64(元),所以他购买这件衣服实际用了64元.

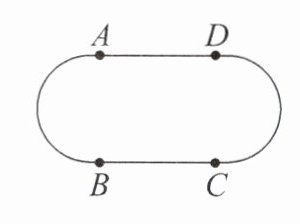
9. 练思维·分类讨论 如图,ABCD是400 m的环形跑道,现在把跑道分成相等的4段,即两条直道和两条弯道长度都相同.甲、乙两人沿着环形跑道ABCD练习跑步(匀速),甲从点A出发,乙从点B出发,甲比乙每秒多跑1 m.
(1)如果甲按顺时针方向跑,同时乙按逆时针方向跑,经过25 s两人第一次相遇,求甲、乙两人的速度；
(2)如果两人按(1)中的速度,沿相同的方向同时起跑,当第一次相遇时,甲在环形跑道ABCD的哪一条直道或弯道上？

......答案 P164

答案：
(1)设乙的速度为x m/s,则甲的速度为(x+1)m/s.由题意,得25(x+x+1)=300,解得x=5.5,所以x+1=5.5+1=6.5.答:甲的速度为6.5 m/s,乙的速度为5.5 m/s.
(2)①当甲、乙两人都按顺时针方向跑步,设第一次相遇时用了y s.由题意,得6.5y-5.5y=300,解得y=300.此时甲跑的路程为6.5×300=1950(m).因为1950=400×4+350,所以甲在弯道AB上.②当甲、乙两人都按逆时针方向跑步,设第一次相遇时用了z s.由题意,得6.5z-5.5z=100,解得z=100.此时甲跑的路程为6.5×100=650(m).因为650=400+250,所以甲在弯道CD上.综上,当甲、乙两人按顺时针方向跑步,当第一次相遇时,甲在弯道AB上;当甲、乙两人按逆时针方向跑步,当第一次相遇时,甲在弯道CD上.