《2025年一本预备新初一小升初数学》

【例6】比较下列各组数的大小:
(1)-9与8;
(2)|7.6|与|-7.6|;
(3)0与-|-7|;
(4)-$\frac{1}{2}$与-$\frac{2}{5}$.
[答案]解:(1)因为正数大于负数,所以-9＜8.
(2)先求绝对值,|7.6|= 7.6,|-7.6|= 7.6.
因为7.6= 7.6,所以|7.6|= |-7.6|.
(3)先化简,-|-7|= -7.
因为0大于负数,所以0＞-7,即0＞-|-7|.
(4)先求绝对值,|-$\frac{1}{2}$|= $\frac{1}{2}$,|-$\frac{2}{5}$|= $\frac{2}{5}$.
因为$\frac{1}{2}$＞$\frac{2}{5}$,所以-$\frac{1}{2}$＜-$\frac{2}{5}$.

答案： 解：
(1)因为正数大于负数，所以-9＜8.
(2)先求绝对值，|7.6|=7.6，|-7.6|=7.6.
因为7.6=7.6，所以|7.6|=|-7.6|.
(3)先化简，-|-7|=-7.
因为0大于负数，所以0＞-7，即0＞-|-7|.
(4)先求绝对值，|-$\frac{1}{2}$|=$\frac{1}{2}$，|-$\frac{2}{5}$|=$\frac{2}{5}$.
因为$\frac{1}{2}$＞$\frac{2}{5}$，所以-$\frac{1}{2}$＜-$\frac{2}{5}$.

【例7】已知a,b是有理数,若a＞0,b＜0,且|a|＜|b|,借助于数轴,试把a,-a,b,-b四个数用"＜"号连接起来.
[答案]解:如图所示.

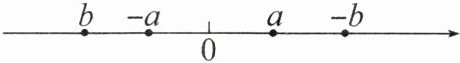
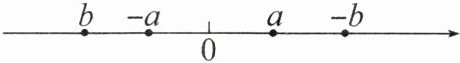
由数轴,得b＜-a＜a＜-b.

答案： 解析：本题考查绝对值的几何意义以及利用数轴比较数的大小。
已知$a\gt0$，$b\lt0$，且$\vert a\vert\lt\vert b\vert$。
在数轴上，正数在$0$的右边，负数在$0$的左边，所以$a$在$0$的右边，$b$在$0$的左边。
$\vert a\vert$表示$a$到$0$的距离，$\vert b\vert$表示$b$到$0$的距离，因为$\vert a\vert\lt\vert b\vert$，所以$b$到$0$的距离比$a$到$0$的距离远。
$-a$是$a$的相反数，在数轴上$-a$与$a$关于原点对称，所以$-a$在$0$的左边；$-b$是$b$的相反数，$-b$在$0$的右边。
根据上述分析，在数轴上从左到右的顺序为$b\lt -a\lt a\lt -b$。
答案：$b\lt -a\lt a\lt -b$。

【练8】下列有理数的大小关系判断正确的是(A)
A.-$\frac{6}{7}$＜-$\frac{5}{6}$
B.-|$\frac{1}{3}$|＞0
C.-$\frac{3}{5}$＞-$\frac{2}{7}$
D.-1＞-0.01

答案： A [解析] A.因为$-\frac{6}{7}=-\frac{36}{42}$,$-\frac{5}{6}=-\frac{35}{42}$,$\frac{36}{42}＞\frac{35}{42}$,所以$-\frac{6}{7}＜-\frac{5}{6}$,故A正确;B.因为$-|\frac{1}{3}|=-\frac{1}{3}＜0$,所以$-|\frac{1}{3}|＜0$,故B错误;C.因为$-\frac{3}{5}=-\frac{21}{35}$,$-\frac{2}{7}=-\frac{10}{35}$,$\frac{21}{35}＞\frac{10}{35}$,所以$-\frac{3}{5}＜-\frac{2}{7}$,故C错误;D.因为$1＞0.01$,所以$-1＜-0.01$,故D错误.

【练9】已知有理数a,b,c在数轴上的对应点的位置如图所示,试比较a,b,c,-a,-b,-c,0的大小,并用"＜"号连接起来.

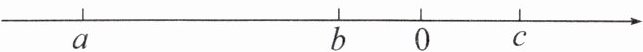
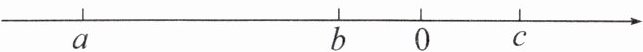
答案： 解:由题中数轴可知$a＜ b＜0＜ c$,且$|a|＞|c|＞|b|$,所以$a＜-c＜ b＜0＜-b＜ c＜-a$.