《2025年一本预备新初一小升初数学》

1.下列说法中,正确的是 (C)
A.两条射线组成的图形叫作角
B.有公共端点的两条线段组成的图形叫作角
C.角可以看作是由一条射线绕着它的端点旋转而形成的图形
D.角的边越长,角越大

答案： C

2.如图,下列表示角的方法错误的是 (C)
A.$∠1与∠AOB$表示同一个角
B.$∠β表示的是∠BOC$
C.$∠AOC也可用∠O$来表示
D.图中共有三个角：$∠AOB$,$∠AOC$,$∠BOC$

答案： C [解析] 当以某一个字母表示的点为顶点的角只有一个时，才可以用顶点处的字母表示这个角，所以∠AOC 不可以用∠O 来表示，故 C 选项错.

3.(广西中考)如图,10点整时,时针与分针所成的角是 (B)
A.$30^{\circ }$
B.$60^{\circ }$
C.$90^{\circ }$
D.$120^{\circ }$

答案： B [解析] 因为钟面分成 12 个大格，每个大格的度数是 30°，所以 10 点整时，时针与分针所成的角是 60°.

4.如图,写出符合下列条件的角.
(1)能用一个大写字母表示的角：∠A，∠C；
(2)以B为顶点的角：∠ABE，∠ABC，∠EBC；
(3)图中共有7个小于平角的角.

答案：
(1)∠A，∠C
(2)∠ABE，∠ABC，∠EBC
(3)7

5.已知某学校下午上课的时间为14时20分,则此时钟表上的时针与分针的夹角为(B)
A.$40^{\circ }$
B.$50^{\circ }$
C.$60^{\circ }$
D.$70^{\circ }$

答案： B [解析] 因为 14 时 20 分时，时针指向 2 和 3 之间，分针指向 4，所以时针与分针的夹角为 2×30°-20×0.5°=50°.

6.(1)用度表示$37^{\circ }24'36''$；
(2)用度、分、秒表示$48.26^{\circ }$.

答案： 解：
(1)37°24'36''=37°+24'+36''=37°+24'+36×(1/60)'=37°+24'+0.6'=37°24.6'=37°+24.6×(1/60)°=37°+0.41°=37.41°.
(2)48.26°=48°+0.26°=48°+0.26×60'=48°+15.6'=48°+15'+0.6×60''=48°+15'+36''=48°15'36''.

7.练思维·规律探究 如图,从点O引出的射线(任意2条不共线)条数与角的总个数有如下关系：如图1,从点O引出2条射线共形成1个角；如图2,从点O引出3条射线共形成3个角；如图3,从点O引出4条射线共形成6个角；如图4,从点O引出5条射线共形成10个角.

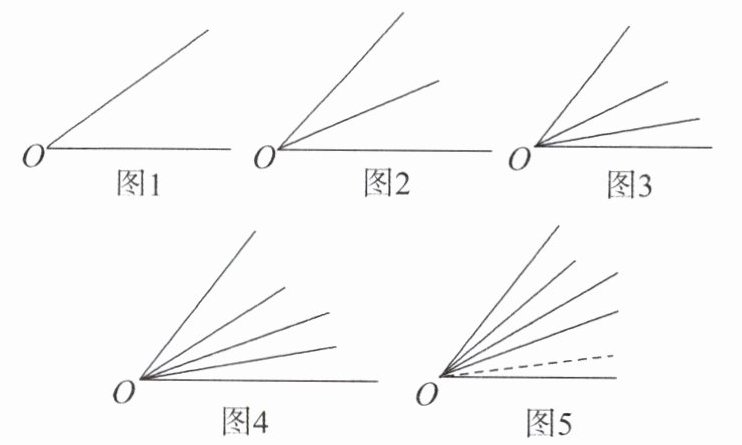
(1)观察操作：当从点O引出6条射线时,共形成______个角.15
(2)探索发现：如图5,当从点O引出n条射线时,共形成______个角.(用含n的式子表示)n(n-1)/2
(3)实践应用：8支篮球队进行单循环比赛(参加比赛的每两支球队之间都要进行一场比赛),求总的比赛场数.如果n支篮球队进行主客场制单循环赛(参加比赛的每支球队都与其他所有队各赛2场),那么总的比赛场数是多少？将每支球队当作一条射线，每场单循环赛当作一个角，所以8支篮球队进行单循环比赛相当于8条射线可以形成的角，所以总的比赛场数为8×(8-1)/2=28。如果n支篮球队进行主客场制单循环赛(参加比赛的每支球队都与其他所有各队赛2场)，那么总的比赛场数是n(n-1)/2×2=n(n-1)。

答案： 解：
(1)观察题图可知，2 条射线形成 1 个角，3 条射线形成 2+1=3(个)角，4 条射线形成 3+2+1=6(个)角，由此可得，6 条射线形成角的个数是 1+2+3+4+5=15. 故答案为 15.
(2)根据
(1)中的规律可知，n 条射线形成角的个数是1+2+3+…+(n-1)=n(n-1)/2. 故答案为n(n-1)/2.
(3)将每支球队当作一条射线，每场单循环赛当作一个角，所以 8 支篮球队进行单循环比赛相当于 8 条射线可以形成的角，所以总的比赛场数为8×(8-1)/2=28.如果 n 支篮球队进行主客场制单循环赛(参加比赛的每支球队都与其他所有各队赛 2 场)，那么总的比赛场数是n(n-1)/2×2=n(n-1).