《2025年一本预备新初一小升初数学》

【例3】如图,直线上有 A,B,C,D 四点.①AC= AB+BC；②CD= AD-AC；③AC+BD-BC= AD.

答案： 解析：本题主要考查对直线、射线、线段的理解以及线段之间的长度关系。
①$AC$的长度是由$A$点到$C$点的距离，这个距离可以看作是$A$点到$B$点的距离（即$AB$）加上$B$点到$C$点的距离（即$BC$）。
所以，$AC = AB + BC$。
②$CD$的长度可以由$A$点到$D$点的距离（即$AD$）减去$A$点到$C$点的距离（即$AC$）得到。
所以，$CD = AD - AC$。
③$AC + BD - BC$可以看作是$A$到$C$的距离加上$B$到$D$的距离，然后减去$B$到$C$的距离。这实际上等于$A$到$D$的距离，因为$AC + BD - BC = AD$（可以理解为从$A$到$C$，再从$C$到$D$（即$BD$中$C$到$D$的部分），然后减去重复的$B$到$C$的部分）。
所以，$AC + BD - BC = AD$。
答案：①$AB$；②$AC$；③$AD$。

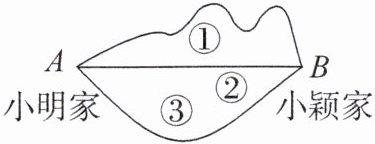
【例4】如图,小明家到小颖家有三条路,若小明想尽快到达小颖家,他应该选线路②,用数学知识解释为两点之间,线段最短.

答案： 解析：本题考查线段的基本性质。在连接两点的所有线中，线段是最短的，它是在解决最短路径问题时常用的数学原理。题目中小明家到小颖家有三条路，而线路②是线段，根据“两点之间，线段最短”的原理，线路②是最短的路线。
答案：②；两点之间，线段最短。

(1)BD= CD+BC；(2)CE=CD+DE；
(3)BE= BC+CD+DE；(4)BD= AD-AB= BE-DE.

答案：
(1)BC　
(2)CD　DE　
(3)CD　
(4)AB　DE

【练7】有下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上；②植树时,只要定出两棵树的位置,就能确定这一行树所在的直线；③从 A 地到 B 地,架设电线,总是尽可能沿着线段 AB 架设；④把弯曲的公路改直,就能缩短路程.其中可以用“两点之间,线段最短”来解释的现象有③④.(填序号)

答案： ③④ [解析]①②现象可以用“两点确定一条直线”来解释.

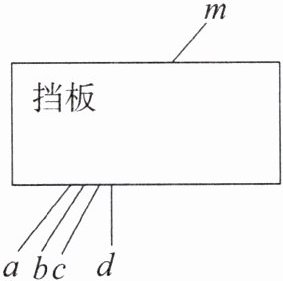
1.(河北中考)如图,已知四条线段a,b,c,d中的一条与挡板另一侧的线段m在同一条直线上,请借助直尺判断该线段是 (A)

A.a
B.b
C.c
D.d

答案： A

2.下列说法正确的是 (C)
A.延长线段AB和延长线段BA的含义相同
B.射线AB和射线BA是同一条射线
C.经过两点可以画一条直线,并且只能画一条直线
D.延长直线AB

答案： C [解析] A.端点不同，含义不同，故 A 选项错误；B.射线 AB 和射线 BA 的端点不同，所以不是同一条射线，故 B 选项错误；D.直线向两个方向无限延伸，所以不能延长，故 D 选项错误.

3.如图,经过刨平的木板上的A,B两点,能且只能弹出一条笔直的墨线,依据是 (B)

A.两点之间,线段最短
B.两点确定一条直线
C.过一点,有无数条直线
D.连接两点之间的线段的长度,叫作两点之间的距离

答案： B [解析] 因为经过两点有一条直线，并且只有一条直线，所以经过木板上的 A,B 两点，只能弹出一条笔直的墨线.