《2025年暑假Happy假日七年级数学北师大版》

11. 杜牧《清明》诗中写道“清明时节雨纷纷”,从数学的观点看,诗句中描述的事件是______(填“必然”或“随机”)事件。

答案： 随机

12. 小芳掷一枚质地均匀的硬币10次,有7次正面向上,当她掷第11次时,正面向上的概率为______。

答案： $\frac{1}{2}$

13. 一个正方体木块,六个面上分别写有数字2,3,5,6,7,9,小光、小亮两人随意往桌面上扔放这个木块。规定:当小光扔时,如果朝上的一面写的是偶数,得1分;当小亮扔时,如果朝上的一面写的是奇数,得1分。每人扔100次,______得分高的可能性比较大。

答案： 小亮

14. 在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有3个红球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复试验后发现,摸到红球的频率稳定于0.2,那么可以推算出n大约是______。

答案： $15$

15. 某鱼塘养了1000条鲤鱼、若干条草鱼和500条罗非鱼,该鱼塘主通过多次捕捞试验后发现,捕捞到草鱼的频率稳定在0.5左右,若该鱼塘主随机在鱼塘捕捞一条鱼,则捞到鲤鱼的概率约为______。

答案： $\frac{1}{3}$

16. 如图,把一个圆形转盘按1:2:3:4的比例分成A,B,C,D四个扇形区域,自由转动转盘,停止后指针落在C区域的概率是______。

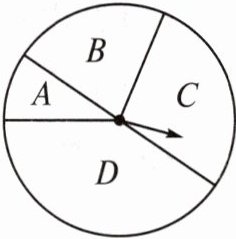
答案： $\frac{3}{10}$

17. (6分)在不透明的袋子中装有3个红球和6个黄球,每个球除颜色外都相同。
(1)从中任意摸出一个球,摸到______球的可能性大;
(2)如果另外拿5个球放入袋中,你认为怎样放才能让摸到红球和黄球的可能性相同?

答案： 【解析】：
1. 首先分析（1）中摸到哪种球的可能性大小：
可能性大小与球的数量有关，在不透明袋子中，哪种颜色球的数量越多，摸到的可能性就越大。
已知袋子中装有$3$个红球和$6$个黄球，因为$6\gt3$，即黄球的数量多于红球的数量。
所以从中任意摸出一个球，摸到黄球的可能性大。
2. 然后分析（2）中如何放球使摸到红球和黄球的可能性相同：
要使摸到红球和黄球的可能性相同，则红球和黄球的数量应相等。
设放入$x$个红球，则放入$(5 - x)$个黄球。
原来有$3$个红球和$6$个黄球，放入球后红球有$(3 + x)$个，黄球有$(6+(5 - x))$个。
令$3 + x=6+(5 - x)$，
去括号得$3 + x=6 + 5 - x$。
移项得$x+x=6 + 5 - 3$。
合并同类项得$2x=8$。
系数化为$1$得$x = 4$。
那么$5 - x=5 - 4 = 1$。
即放入$4$个红球，$1$个黄球时，摸到红球和黄球的可能性相同。
【答案】：（1）黄；（2）放入$4$个红球，$1$个黄球