2025年小题狂做高中数学必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第91页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
8. 已知正方体 $ ABCD - A_1B_1C_1D_1 $ 的棱长为 2,点 $ P $ 为正方形 $ BCC_1B_1 $ 内(包括边)一动点,则下列说法正确的是(
A.对于任意点 $ P $,均有平面 $ A_1D_1P \perp $ 平面 $ ABB_1A_1 $
B.当点 $ P $ 在线段 $ B_1C_1 $ 上时,平面 $ A_1D_1P $ 与平面 $ A_1BCD_1 $ 所成二面角的大小为 $ 60° $
C.当点 $ P $ 在线段 $ B_1C $ 上时,$ A_1P \perp BC_1 $
D.当点 $ P $ 为线段 $ BC_1 $ 的中点时,三棱锥 $ A_1 - B_1D_1P $ 的体积为 $ \frac{2}{3} $
ACD
)A.对于任意点 $ P $,均有平面 $ A_1D_1P \perp $ 平面 $ ABB_1A_1 $
B.当点 $ P $ 在线段 $ B_1C_1 $ 上时,平面 $ A_1D_1P $ 与平面 $ A_1BCD_1 $ 所成二面角的大小为 $ 60° $
C.当点 $ P $ 在线段 $ B_1C $ 上时,$ A_1P \perp BC_1 $
D.当点 $ P $ 为线段 $ BC_1 $ 的中点时,三棱锥 $ A_1 - B_1D_1P $ 的体积为 $ \frac{2}{3} $
答案:
8.ACD 如图所示,
由正方体的性质可知,$A_{1}D_{1}\perp$平面$ABB_{1}A_{1}$,又$A_{1}D_{1}\subset$平面$A_{1}D_{1}P$,所以对于任意点$P$,均有平面$A_{1}D_{1}P\perp$平面$ABB_{1}A_{1}$,故A正确;$A_{1}B_{1}\perp A_{1}D_{1}$,$A_{1}B_{1}\perp A_{1}A$,所以$\angle BA_{1}B_{1}$即为平面$A_{1}D_{1}P$与平面$A_{1}BCD_{1}$所成二面角的平面角,为$45^{\circ}$,故B错误;因为$A_{1}B_{1}\perp$平面$BCC_{1}B_{1}$,$BC\subset$平面$BCC_{1}B_{1}$,所以$A_{1}B_{1}\perp BC$,又$BC\perp B_{1}C_{1}$,且$A_{1}B_{1}\cap B_{1}C_{1}=B_{1}$,$A_{1}B_{1}$,$BC\subset$平面$A_{1}B_{1}P$,所以$BC\perp$平面$A_{1}B_{1}P$,因为$A_{1}P\subset$平面$A_{1}B_{1}P$,所以$BC\perp A_{1}P$,故C正确;当点$P$为线段$B_{1}C$的中点时,点$P$到平面$A_{1}B_{1}C_{1}D_{1}$的距离为$1$,则$V_{A_{1}-B_{1}D_{1}P}=V_{P - A_{1}B_{1}D_{1}}=\frac{1}{3}×\frac{1}{2}×2×2×1=\frac{2}{3}$,故D正确。
8.ACD 如图所示,

由正方体的性质可知,$A_{1}D_{1}\perp$平面$ABB_{1}A_{1}$,又$A_{1}D_{1}\subset$平面$A_{1}D_{1}P$,所以对于任意点$P$,均有平面$A_{1}D_{1}P\perp$平面$ABB_{1}A_{1}$,故A正确;$A_{1}B_{1}\perp A_{1}D_{1}$,$A_{1}B_{1}\perp A_{1}A$,所以$\angle BA_{1}B_{1}$即为平面$A_{1}D_{1}P$与平面$A_{1}BCD_{1}$所成二面角的平面角,为$45^{\circ}$,故B错误;因为$A_{1}B_{1}\perp$平面$BCC_{1}B_{1}$,$BC\subset$平面$BCC_{1}B_{1}$,所以$A_{1}B_{1}\perp BC$,又$BC\perp B_{1}C_{1}$,且$A_{1}B_{1}\cap B_{1}C_{1}=B_{1}$,$A_{1}B_{1}$,$BC\subset$平面$A_{1}B_{1}P$,所以$BC\perp$平面$A_{1}B_{1}P$,因为$A_{1}P\subset$平面$A_{1}B_{1}P$,所以$BC\perp A_{1}P$,故C正确;当点$P$为线段$B_{1}C$的中点时,点$P$到平面$A_{1}B_{1}C_{1}D_{1}$的距离为$1$,则$V_{A_{1}-B_{1}D_{1}P}=V_{P - A_{1}B_{1}D_{1}}=\frac{1}{3}×\frac{1}{2}×2×2×1=\frac{2}{3}$,故D正确。
9. 在四边形 $ ABCD $ 中,$ AD // BC $,$ AD = AB $,$ \angle BCD = 45° $,$ \angle BAD = 90° $,将 $ \triangle ABD $ 折起,使平面 $ ABD \perp $ 平面 $ BCD $,构成三棱锥 $ A - BCD $,如图,在三棱锥 $ A - BCD $ 中,下列结论正确的是(
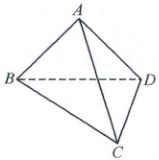
A.$ CD \perp AB $
B.$ CD \perp BD $
C.平面 $ ABC \perp $ 平面 $ BDC $
D.平面 $ ADC \perp $ 平面 $ ABD $
ABD
)
A.$ CD \perp AB $
B.$ CD \perp BD $
C.平面 $ ABC \perp $ 平面 $ BDC $
D.平面 $ ADC \perp $ 平面 $ ABD $
答案:
9.ABD 对于B,如图1,因为$AD// BC$,$AD=AB$,$\angle BAD=90^{\circ}$,所以$\angle ABD=\angle ADB=45^{\circ}$,又因为$\angle BCD=45^{\circ}$,$AD// BC$,所以$\angle ADC=135^{\circ}$,所以$\angle BDC=\angle ADC-\angle ADB=135^{\circ}-45^{\circ}=90^{\circ}$,即$CD\perp BD$,故B正确;对于A,由B选项知$CD\perp BD$,又因为平面$ABD\perp$平面$BCD$,$CD\subset$平面$BCD$,平面$ABD\cap$平面$BCD=BD$,所以$CD\perp$平面$ABD$,因为$AB\subset$平面$ABD$,所以$CD\perp AB$,故A正确;对于D,由选项A知,$CD\perp$平面$ABD$,因为$CD\subset$平面$ADC$,所以平面$ADC\perp$平面$ABD$,故D正确;对于C,如图2,过点$A$作$AE\perp BD$,垂足为$E$,因为平面$ABD\perp$平面$BCD$,$AE\subset$平面$ABD$,平面$ABD\cap$平面$BCD=BD$,所以$AE\perp$平面$BCD$,显然$AE\subset$平面$ABC$,所以平面$ABC$与平面$BDC$不垂直,故C错误。

9.ABD 对于B,如图1,因为$AD// BC$,$AD=AB$,$\angle BAD=90^{\circ}$,所以$\angle ABD=\angle ADB=45^{\circ}$,又因为$\angle BCD=45^{\circ}$,$AD// BC$,所以$\angle ADC=135^{\circ}$,所以$\angle BDC=\angle ADC-\angle ADB=135^{\circ}-45^{\circ}=90^{\circ}$,即$CD\perp BD$,故B正确;对于A,由B选项知$CD\perp BD$,又因为平面$ABD\perp$平面$BCD$,$CD\subset$平面$BCD$,平面$ABD\cap$平面$BCD=BD$,所以$CD\perp$平面$ABD$,因为$AB\subset$平面$ABD$,所以$CD\perp AB$,故A正确;对于D,由选项A知,$CD\perp$平面$ABD$,因为$CD\subset$平面$ADC$,所以平面$ADC\perp$平面$ABD$,故D正确;对于C,如图2,过点$A$作$AE\perp BD$,垂足为$E$,因为平面$ABD\perp$平面$BCD$,$AE\subset$平面$ABD$,平面$ABD\cap$平面$BCD=BD$,所以$AE\perp$平面$BCD$,显然$AE\subset$平面$ABC$,所以平面$ABC$与平面$BDC$不垂直,故C错误。


10. 已知 $ l $ 是平面 $ \beta $ 外的一条直线,$ \alpha $ 是一个平面. 给出下列三个论断:① $ \alpha \perp \beta $;② $ l \perp \alpha $;③ $ l // \beta $. 以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:
①②⇒③或②③⇒①
.
答案:
10.①②$\Rightarrow$③或②③$\Rightarrow$①
(1)①②$\Rightarrow$③,证明:因为$\alpha\perp\beta$,$l\perp\alpha$,所以$l//\beta$或$l\subset\beta$,又$l$是平面$\beta$外的一条直线,所以$l//\beta$,命题正确。
(2)①③$\Rightarrow$②,证明:设$\alpha\cap\beta=m$,取直线$l// m$,此时$l//\beta$,但直线$l$可能与平面$\alpha$平行,也可能在平面$\alpha$内,所以命题不正确。
(3)②③$\Rightarrow$①,证明:因为$l//\beta$,所以平面$\beta$内必存在一条直线与直线$l$平行,设为$n$,即$n// l$,又因为$l\perp\alpha$,所以$n\perp\alpha$,从而得$\alpha\perp\beta$,所以命题正确。
(1)①②$\Rightarrow$③,证明:因为$\alpha\perp\beta$,$l\perp\alpha$,所以$l//\beta$或$l\subset\beta$,又$l$是平面$\beta$外的一条直线,所以$l//\beta$,命题正确。
(2)①③$\Rightarrow$②,证明:设$\alpha\cap\beta=m$,取直线$l// m$,此时$l//\beta$,但直线$l$可能与平面$\alpha$平行,也可能在平面$\alpha$内,所以命题不正确。
(3)②③$\Rightarrow$①,证明:因为$l//\beta$,所以平面$\beta$内必存在一条直线与直线$l$平行,设为$n$,即$n// l$,又因为$l\perp\alpha$,所以$n\perp\alpha$,从而得$\alpha\perp\beta$,所以命题正确。
11. 在四棱锥 $ P - ABCD $ 中,底面 $ ABCD $ 为矩形,$ \triangle PCD $ 是等边三角形,平面 $ PCD \perp $ 底面 $ ABCD $,$ AD = 3 $,四棱锥 $ P - ABCD $ 的体积为 $ 18\sqrt{3} $. 若 $ E $ 是 $ PC $ 的中点,则线段 $ DE $ 的长为
3\sqrt{3}
.
答案:
11.$3\sqrt{3}$ 如图所示,设$AB=CD=2a$,则矩形$ABCD$的面积$S_{矩形ABCD}=3×2a=6a$。取$CD$的中点$F$,连接$PF$,由$\triangle PCD$是等边三角形,得$PF\perp CD$,且$PF=\sqrt{3}a$。因为平面$PCD\perp$平面$ABCD$,平面$PCD\cap$平面$ABCD=CD$,$PF\subset$平面$PCD$,所以$PF\perp$平面$ABCD$,即$PF$是四棱锥$P - ABCD$的高,所以四棱锥$P - ABCD$的体积$V_{四棱锥P - ABCD}=\frac{1}{3}S_{矩形ABCD}· PF=\frac{1}{3}×6a×\sqrt{3}a = 18\sqrt{3}$,解得$a = 3$,所以$PF=\sqrt{3}a=3\sqrt{3}$。
11.$3\sqrt{3}$ 如图所示,设$AB=CD=2a$,则矩形$ABCD$的面积$S_{矩形ABCD}=3×2a=6a$。取$CD$的中点$F$,连接$PF$,由$\triangle PCD$是等边三角形,得$PF\perp CD$,且$PF=\sqrt{3}a$。因为平面$PCD\perp$平面$ABCD$,平面$PCD\cap$平面$ABCD=CD$,$PF\subset$平面$PCD$,所以$PF\perp$平面$ABCD$,即$PF$是四棱锥$P - ABCD$的高,所以四棱锥$P - ABCD$的体积$V_{四棱锥P - ABCD}=\frac{1}{3}S_{矩形ABCD}· PF=\frac{1}{3}×6a×\sqrt{3}a = 18\sqrt{3}$,解得$a = 3$,所以$PF=\sqrt{3}a=3\sqrt{3}$。

12. 如图,四棱锥 $ P - ABCD $ 的一个侧面 $ PAD $ 为等边三角形,且平面 $ PAD \perp $ 平面 $ ABCD $,四边形 $ ABCD $ 是平行四边形,$ AD = 2 $,$ BD = 2\sqrt{3} $,$ \angle BAD = \frac{\pi}{3} $,则四棱锥 $ P - ABCD $ 的高为
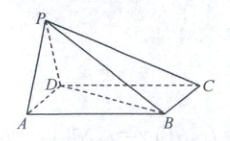
\sqrt{3}
;二面角 $ P - BC - D $ 的余弦值为\frac{2\sqrt{5}}{5}
.
答案:
12.$\frac{2\sqrt{5}}{5}$ 如图,作$PO\perp AD$于点$O$,则$PO\perp$平面$ABCD$,即$PO$为$P - ABCD$的高。$PO=\sqrt{PD^{2}-(\frac{AD}{2})^{2}}=\sqrt{3}$,所以四棱锥$P - ABCD$的高为$\sqrt{3}$。过点$O$作$OE\perp BC$于点$E$,连接$PE$,设平面$DBC$与平面$PBC$所成二面角的平面角为$\theta$,由余弦定理可得$BD^{2}=AD^{2}+AB^{2}-2AD· AB\cos\angle BAD$,即$12 = 4 + AB^{2}-2AB$,解得$AB = 4$,故$AB^{2}=AD^{2}+BD^{2}$,即$AD\perp DB$。又$PO\perp$平面$ABCD$,则$PO\perp EC$,$PO\cap OE=O$,则$EC\perp$平面$POE$,所以$\angle PEO$为二面角$P - BC - D$的平面角,又$PO=\sqrt{3}$,$OE = BD = 2\sqrt{3}$,所以$\tan\theta=\frac{PO}{OE}=\frac{1}{2}$,则$\cos\theta=\frac{2\sqrt{5}}{5}$,所以二面角$P - BC - D$的余弦值为$\frac{2\sqrt{5}}{5}$。
12.$\frac{2\sqrt{5}}{5}$ 如图,作$PO\perp AD$于点$O$,则$PO\perp$平面$ABCD$,即$PO$为$P - ABCD$的高。$PO=\sqrt{PD^{2}-(\frac{AD}{2})^{2}}=\sqrt{3}$,所以四棱锥$P - ABCD$的高为$\sqrt{3}$。过点$O$作$OE\perp BC$于点$E$,连接$PE$,设平面$DBC$与平面$PBC$所成二面角的平面角为$\theta$,由余弦定理可得$BD^{2}=AD^{2}+AB^{2}-2AD· AB\cos\angle BAD$,即$12 = 4 + AB^{2}-2AB$,解得$AB = 4$,故$AB^{2}=AD^{2}+BD^{2}$,即$AD\perp DB$。又$PO\perp$平面$ABCD$,则$PO\perp EC$,$PO\cap OE=O$,则$EC\perp$平面$POE$,所以$\angle PEO$为二面角$P - BC - D$的平面角,又$PO=\sqrt{3}$,$OE = BD = 2\sqrt{3}$,所以$\tan\theta=\frac{PO}{OE}=\frac{1}{2}$,则$\cos\theta=\frac{2\sqrt{5}}{5}$,所以二面角$P - BC - D$的余弦值为$\frac{2\sqrt{5}}{5}$。

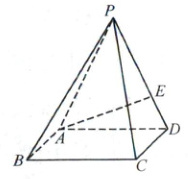
13. 如图所示,在四棱锥 $ P - ABCD $ 中,底面 $ ABCD $ 是边长 2 的正方形,侧面 $ PAD $ 为等腰三角形,$ PA = PD = 4 $,侧面 $ PAD \perp $ 底面 $ ABCD $.
(1)在线段 $ PD $ 上是否存在一点 $ E $,使得 $ AE \perp PC $? 若存在,请求出 $ \frac{PE}{ED} $ 的值;若不存在,请说明理由.
(2)求二面角 $ P - BC - A $ 的余弦值.
(1)在线段 $ PD $ 上是否存在一点 $ E $,使得 $ AE \perp PC $? 若存在,请求出 $ \frac{PE}{ED} $ 的值;若不存在,请说明理由.
(2)求二面角 $ P - BC - A $ 的余弦值.

答案:
13.解:
(1)存在点$E$满足条件,且$\frac{PE}{ED}=7$。
证明:因为底面$ABCD$为正方形,所以$CD\perp AD$。因为侧面$PAD\perp$底面$ABCD$,侧面$PAD\cap$底面$ABCD=AD$,$CD\subset$平面$ABCD$,所以$CD\perp$平面$PAD$。又$AE\subset$平面$PAD$,所以$CD\perp AE$。而$PC\cap CD=C$,$CD\subset$平面$PCD$,$PC\subset$平面$PCD$,要使$AE\perp PC$,则必有$AE\perp$平面$PCD$。因为$PD\subset$平面$PCD$,所以$AE\perp PD$。在等腰三角形$PAD$中,$PA = PD = 4$,$AD = 2$,计算可得$AE=\frac{\sqrt{15}}{2}$,$DE=\frac{1}{2}$,所以$PE=PD - DE=\frac{7}{2}$,所以$\frac{PE}{ED}=7$。
(2)设$AD$的中点为$O$,连接$PO$,如图。因为$PA = PD$,所以$PO\perp AD$。取$BC$的中点$F$,连接$PF$,$OF$。因为$PO\perp AD$,$BC// AD$,所以$PO\perp BC$;因为$OF\perp BC$,$PO\cap OF=O$,$PO$,$OF\subset$平面$POF$,所以$BC\perp$平面$POF$;又$PF\subset$平面$POF$,所以$BC\perp PF$,所以$\angle PFO$是所求二面角的平面角。因为$\triangle PAD$为等腰三角形,且$PA = PD = 4$,底面$ABCD$是边长为$2$的正方形,所以$PO=\sqrt{15}$,$FO = 2$。因为$PO\perp AD$,侧面$PAD\perp$底面$ABCD$,侧面$PAD\cap$底面$ABCD=AD$,$PO\subset$平面$PAD$,所以$PO\perp$底面$ABCD$。因为$OF\subset$底面$ABCD$,所以$PO\perp OF$。在$Rt\triangle POF$中,$PF^{2}=PO^{2}+OF^{2}$,所以$PF=\sqrt{19}$,所以$\cos\angle PFO=\frac{OF}{PF}=\frac{2}{\sqrt{19}}=\frac{2\sqrt{19}}{19}$。故二面角$P - BC - A$的余弦值为$\frac{2\sqrt{19}}{19}$。
13.解:
(1)存在点$E$满足条件,且$\frac{PE}{ED}=7$。
证明:因为底面$ABCD$为正方形,所以$CD\perp AD$。因为侧面$PAD\perp$底面$ABCD$,侧面$PAD\cap$底面$ABCD=AD$,$CD\subset$平面$ABCD$,所以$CD\perp$平面$PAD$。又$AE\subset$平面$PAD$,所以$CD\perp AE$。而$PC\cap CD=C$,$CD\subset$平面$PCD$,$PC\subset$平面$PCD$,要使$AE\perp PC$,则必有$AE\perp$平面$PCD$。因为$PD\subset$平面$PCD$,所以$AE\perp PD$。在等腰三角形$PAD$中,$PA = PD = 4$,$AD = 2$,计算可得$AE=\frac{\sqrt{15}}{2}$,$DE=\frac{1}{2}$,所以$PE=PD - DE=\frac{7}{2}$,所以$\frac{PE}{ED}=7$。
(2)设$AD$的中点为$O$,连接$PO$,如图。因为$PA = PD$,所以$PO\perp AD$。取$BC$的中点$F$,连接$PF$,$OF$。因为$PO\perp AD$,$BC// AD$,所以$PO\perp BC$;因为$OF\perp BC$,$PO\cap OF=O$,$PO$,$OF\subset$平面$POF$,所以$BC\perp$平面$POF$;又$PF\subset$平面$POF$,所以$BC\perp PF$,所以$\angle PFO$是所求二面角的平面角。因为$\triangle PAD$为等腰三角形,且$PA = PD = 4$,底面$ABCD$是边长为$2$的正方形,所以$PO=\sqrt{15}$,$FO = 2$。因为$PO\perp AD$,侧面$PAD\perp$底面$ABCD$,侧面$PAD\cap$底面$ABCD=AD$,$PO\subset$平面$PAD$,所以$PO\perp$底面$ABCD$。因为$OF\subset$底面$ABCD$,所以$PO\perp OF$。在$Rt\triangle POF$中,$PF^{2}=PO^{2}+OF^{2}$,所以$PF=\sqrt{19}$,所以$\cos\angle PFO=\frac{OF}{PF}=\frac{2}{\sqrt{19}}=\frac{2\sqrt{19}}{19}$。故二面角$P - BC - A$的余弦值为$\frac{2\sqrt{19}}{19}$。

查看更多完整答案,请扫码查看


